《2026年授之以渔河北各地市中考试题汇编数学》

19. (本小题满分8分)
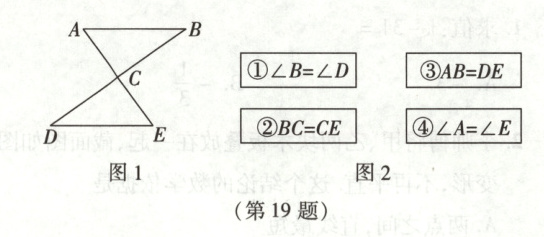
如图1，线段$AE$和$BD$相交于点$C$，连接$AB$，$DE$。四张卡片除正面分别写着如图2所示的四个不同的条件外完全相同，将四张卡片背面朝上洗匀后放在桌面上。
(1)若小明第一次抽到卡片③后，再从剩下的三张卡片中随机抽取一张，则两张卡片上的条件能证明$\triangle BCA\cong\triangle DCE$的概率是$\frac{2}{3}$；
(2)若从四张卡片中随机抽出两张，用画树状图法求两张卡片上的条件能证明$\triangle ABC\cong\triangle EDC$的概率。

答案： 19.解:
(1)$\frac{2}{3}$ ……2分
(2)画树状图如下. ……5分
共有12种等可能的结果，其中4种结果能证明△ABC≌△EDC,分别为①③、③①、③④、④③,
∴P = $\frac{4}{12}=\frac{1}{3}$. ……8分

20. （本小题满分9分）
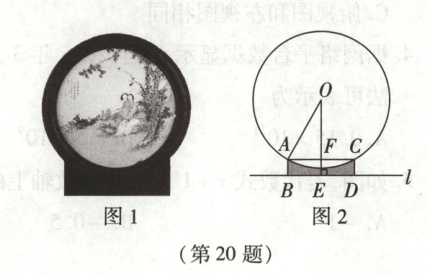
瓷板画（图1）是我国非物质文化遗产，可装裱或嵌入到屏风中，作观赏用。图2为其平面示意图，$A$，$C$为$\odot O$上的两点，连接$OA$，$AC$，$AC// BD$（桌面），$AB$，$CD$分别垂直于直线$l$于$B$，$D$两点，过点$O$作$OE\perp BD$于点$E$，交$AC$于点$F$。已知$AB = CD = 4\sqrt{3} cm$，$AC = 30 cm$，$OE = 19\sqrt{3} cm$。
（1）求半径$OA$的长；
（2）求图2中阴影部分的面积。

答案： 20.解:
(1)
∵AC//BD,OE⊥BD,
∴OF⊥AC.
∵AC = 30cm,
∴$AF = \frac{1}{2}AC = 15cm.$
∵AC//BD,AB⊥BD,EF⊥BD,
∴EF = AB = 4√3cm.
∵OE = 19√3cm,
∴OF = 15√3cm.
∴$OA = \sqrt{OF² + AF²}=30cm. ……5$分
(2)连接OC.S四边形$ABDC = AC·AB = 30×4√3 = 120√3(cm²).S△AOC = \frac{1}{2}AC·OF = \frac{1}{2}×30×15√3 = 225√3(cm²).$
∵OA = OC = AC = 30cm,
∴△OAC为等边三角形.
∴∠AOC = 60°.
∴S扇形$AOC = \frac{60×π×30²}{360}=150π(cm²).$
∴S阴影 = 120√3 + 225√3 - 150π = (345√3 - 150π)cm². ……9分