第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
1. 代数式$-7x$的意义可以是(
A.$-7$与$x$的和
B.$-7$与$x$的差
C.$-7$与$x$的积
D.$-7$与$x$的商
C
)A.$-7$与$x$的和
B.$-7$与$x$的差
C.$-7$与$x$的积
D.$-7$与$x$的商
答案:
1.C
2. 淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西$70^{\circ}$的方向,则淇淇家位于西柏坡的(
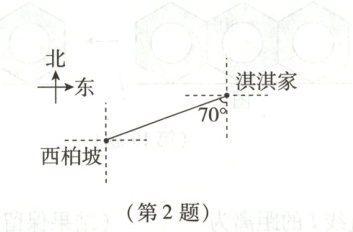
A.南偏西$70^{\circ}$方向
B.南偏东$20^{\circ}$方向
C.北偏西$20^{\circ}$方向
D.北偏东$70^{\circ}$方向
D
)
A.南偏西$70^{\circ}$方向
B.南偏东$20^{\circ}$方向
C.北偏西$20^{\circ}$方向
D.北偏东$70^{\circ}$方向
答案:
2.D
3. 化简$x^{3}(\frac{y^{3}}{x})^{2}$的结果是(
A.$xy^{6}$
B.$xy^{5}$
C.$x^{2}y^{5}$
D.$x^{2}y^{6}$
A
)A.$xy^{6}$
B.$xy^{5}$
C.$x^{2}y^{5}$
D.$x^{2}y^{6}$
答案:
3.A 解析:本题考查幂的运算.$x^{3}(\frac{y^{2}}{x})^{2}=x^{3} · \frac{y^{6}}{x^{2}}=xy^{6}$.故选A.
4. 有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上.若从中随机抽取一张,则抽到的花色可能性

A.(黑桃)
B.(红心)
C.(梅花)
D.(方块)
最
大的是(B
)
A.(黑桃)
B.(红心)
C.(梅花)
D.(方块)
答案:
4.B 解析:本题考查概率.$\because P(抽到黑桃)=\frac{1}{7}$,$P(抽到红心)=\frac{3}{7}$,$P(抽到梅花)=\frac{1}{7}$,$P(抽到方块)=\frac{2}{7}$,$\frac{3}{7}>\frac{2}{7}>\frac{1}{7}=\frac{1}{7}$,$\therefore$抽到的花色可能性最大的是红心.故选B.
5. 四边形$ABCD$的边长如图所示,对角线$AC$的长度随四边形形状的改变而变化.当$\triangle ABC$为等腰三角形时,对角线$AC$的长为(

A.2
B.3
C.4
D.5
B
)
A.2
B.3
C.4
D.5
答案:
5.B 解析:本题考查三角形的三边关系、等腰三角形的性质.在$\triangle ACD$中,$AD = CD = 2$,$\therefore AD - CD < AC < AD + CD$,即$0 < AC < 4$;只有当$AC = AB = 3$时,$\triangle ABC$是等腰三角形.故选B.
6. 若$k$为任意整数,则$(2k + 3)^{2}-4k^{2}$的值总能(
A.被2整除
B.被3整除
C.被5整除
D.被7整除
B
)A.被2整除
B.被3整除
C.被5整除
D.被7整除
答案:
6.B 解析:本题考查平方差公式的应用.原式$=(2k + 3)^{2} - (2k)^{2}=(2k + 3 + 2k)(2k + 3 - 2k)=3(4k + 3)$,$k$为任意整数,$\therefore (2k + 3)^{2} - (2k)^{2}$的值总能被3整除.故选B.
7. 若$a=\sqrt{2},b=\sqrt{7}$,则$\sqrt{\frac{14a^{2}}{b^{2}}}=$(
A.2
B.4
C.$\sqrt{7}$
D.$\sqrt{2}$
A
)A.2
B.4
C.$\sqrt{7}$
D.$\sqrt{2}$
答案:
7.A 解析:本题考查二次根式的运算.$\because a = \sqrt{2}$,$b = \sqrt{7}$,$a^{2} = 2$,$b^{2} = 7$,$\therefore \sqrt{\frac{14a^{2}}{b^{2}}}= \sqrt{\frac{14 × 2}{7}}=\sqrt{4} = 2$.故选A.
查看更多完整答案,请扫码查看


