《2026年授之以渔河北各地市中考试题汇编数学》

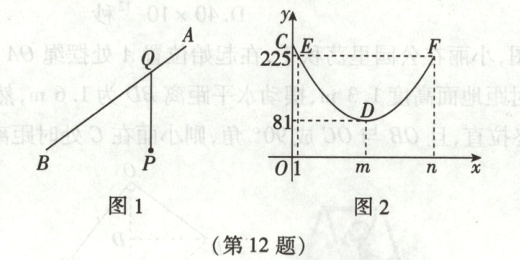
12. (2025·浙江)为了实时规划路径，卫星导航系统需要计算运动点与观测点之间距离的平方。如图1，点$P$是一个固定观测点，运动点$Q$从$A$处出发，沿笔直公路$AB$向目的地$B$处运动。设$AQ = x$(单位：km)$(0 ≤ x ≤ n)$，$PQ^2 = y$(单位：$km^2$)。如图2，$y$关于$x$的函数图象与$y$轴交于点$C$，最低点$D(m, 81)$，且经过$E(1, 225)$和$F(n, 225)$两点，下列选项正确的是(D)

A.$m = 12$
B.$n = 24$
C.点$C$的纵坐标为240
D.点$(15, 85)$在该函数图象上

答案：
12.D 解析：本题考查函数图象、勾股定理、垂线段最短、等腰三角形的性质。如图，作$PG \perp AB$于点$G$，当$x=1$时，动点$Q$运动到点$H$的位置，则由题意和图象可知$PH^{2}=225$，当点$Q$运动到点$G$的位置时，$PQ^{2}$最小，即$PG^{2}=81$，$HG=m - 1$。在$Rt \triangle PGH$中，由勾股定理，得$225=81+(m - 1)^{2}$，$\therefore m=13$(负值已舍去)，故$A$错误。$\therefore AG=13$，$HG=12$。当$x=n$时，点$Q$运动到点$B$的位置，则$PB^{2}=225=PH^{2}$，$\therefore PB=PH$。$\because PG \perp AB$，$\therefore BG=HG=12$，$\therefore AB=AG + BG=25$，即$n=25$，故$B$错误。$\therefore$当$x=0$，即点$Q$在点$A$的位置时，$AP^{2}=AG^{2}+PG^{2}=250$，故$C$错误。点$C$的纵坐标为$250$，故$C$错误。当$x=15$时，点$Q$运动到点$K$的位置，$\therefore AK=15$，$\therefore GK=AK - AG=2$，
$\therefore PK^{2}=KG^{2}+PG^{2}=85$，$\therefore$点$(15,85)$在该函数图象上，故D正确。故选D。

13. (2025·天津)计算$(\sqrt{61} + 1)(\sqrt{61} - 1)$的结果为60。

答案： 13.60

14. (2025·山东东营)如图，在$\triangle ABC$中，$AB = 6$，$\angle BAC = 30^{\circ}$，$\angle BAC$的平分线交$BC$于点$D$，$M$，$N$分别是$AD$和$AB$上的动点，则$BM + MN$的最小值是3。
 

答案：
14.3 解析：本题考查垂线段最短、角平分线的性质、含$30^{\circ }$角的直角三角形的性质。如图，在$AC$上取一点$E$，使$AE=AN$，连接$ME$，$BE$。$\because AD$平分$\angle BAC$，$\therefore \angle MAE=\angle MAN$。又$\because AM=AM$，
$\therefore \triangle MAE \cong \triangle MAN(SAS)$，$\therefore ME=MN$，
$\therefore BM+MN=BM+ME$。$\because$当$B$，$M$，$E$共线，$BE \perp AC$时，$BM+ME$取得最小值，为$BE$的长，此时$BM+MN$也取得最小值。$\because \angle BAC=30^{\circ }$，$\therefore BE=\frac {1} {2}AB=3$，即$BM+MN$的最小值为$3$。

15. (2025·四川成都)从$-1$，$1$，$2$这三个数中任取两个数分别作为$a$，$b$的值，则关于$x$的一元二次方程$ax^2 + bx + 1 = 0$有实数根的概率为$\frac {1} {2}$。

答案：
15.$\frac {1} {2}$ 解析：本题考查一元二次方程根的判别式、概率。画树状图如下，共有$6$种等可能的结果，其中能使该一元二次方程有实数根的结果有$3$种，$\therefore$关于$x$的一元二次方程$ax^{2}+bx+1=0$有实数根的概率为$\frac {3} {6}=\frac {1} {2}$。

16. (2025·浙江)如图，矩形$ABCD$内接于$\odot O$，$E$是$\overset{\frown}{AD}$上一点，连接$EB$，$EC$分别交$AD$于点$F$，$G$。若$AF = 1$，$EG = FG = 3$，则$\odot O$的直径为$2 \sqrt {14}$。

答案：
16.$2 \sqrt {14}$ 解析：本题考查圆的性质、矩形的性质、等腰三角形的性质、全等三角形的判定及性质。如图，连接$AC$，$AE$，记$AC$与$BE$的交点为$L$。$\because$四边形$ABCD$是矩形，且矩形内接于$\odot O$，$\therefore \angle D=\angle BAD=90^{\circ }$，$\therefore AC$是$\odot O$的直径。$\because EG=FG=3$，$\therefore \angle BEC=\angle GFE=\angle AFB$。$\because \angle BEC=\angle BAC$，$\therefore \angle AFB=\angle BAC$，$\angle ALB=\angle GAC+\angle AFB=\angle GAC+\angle BAC=\angle BAD=90^{\circ }$，$\therefore \angle GAC=\angle ABE=90^{\circ }-\angle BAC$。
$\because \angle ABE=\angle ACG$，$\therefore \angle GAC=\angle ACG$，$\therefore CG=AG=AF+FG=1+3=4$。$\because \angle CDG=\angle AEG=90^{\circ }$，$\angle CGD=\angle AGE$，$\therefore \triangle CDG \cong \triangle AEG$，
$\therefore DG=EG=3$，$\therefore AD=AG+DG=4+3=7$，
$CD=\sqrt {CG^{2}-DG^{2}}=\sqrt {4^{2}-3^{2}}=\sqrt {7}$，$\therefore AC=\sqrt {AD^{2}+CD^{2}}=\sqrt {7^{2}+(\sqrt {7})^{2}}=2\sqrt {14}$，$\therefore \odot O$的直径为$2\sqrt {14}$。

17. （2025·黑龙江齐齐哈尔）（本小题满分7分）
（1）计算：$\sqrt{9} - |1 - \sqrt{2}| + 2\sin 45^{\circ} - (\frac{1}{3})^{-2}$；
（2）分解因式：$2x^3 - 8x$。

答案： 17.解：
(1)原式$=3-(\sqrt {2}-1)+\sqrt {2}-9$
$=3-\sqrt {2}+1+\sqrt {2}-9$
$=-5$。 4分
(2)原式$=2x(x^{2}-4)$
$=2x(x + 2)(x - 2)$。 7分