《2026年授之以渔河北各地市中考试题汇编数学》

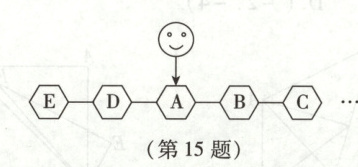
15. (2025·山西)下图是创新小组设计的一款小程序的界面示意图，程序规则为：每点击一次按钮，“”就从一个格子向左或向右随机移动到相邻的一个格子.当“”位于格子$A$时，小明连续点击两次按钮，“”回到格子$A$的概率是$\frac{1}{2}$.

答案：
15.$\frac{1}{2}$ 解析:本题考查概率. 画出树状图如下，由图可知，共有4种等可能的情况，其中回到格子A的情况有2种，则“ ”回到格子A 的概率$P = \frac{2}{4} = \frac{1}{2}$.

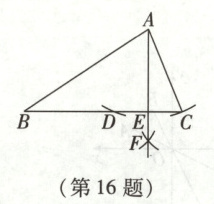
16. (2025·四川广安)如图，在$\triangle ABC$中，按以下步骤作图：(1)以点$A$为圆心，$AC$的长为半径画弧，交$BC$于点$D$；(2)分别以点$C$和点$D$为圆心，大于$\frac{1}{2}CD$的长为半径画弧，两弧相交于点$F$；(3)画射线$AF$交$BC$于点$E$.若$\angle C = 2\angle B$，$BC = 23$，$BD = 13$，则$AE$的长为12.

答案： 16.12 解析:本题考查尺规作图、等腰三角形的判定及性质、三角形外角的性质.
∵BC = 23，BD = 13，
∴CD = 23 - 13 = 10，连接AD，根据作图痕迹可得AD = AC，AE垂直平分CD，
∴∠C = ∠ADC，∠AED = ∠AEC = 90°，DE = CE = $\frac{1}{2}CD = 5$.
∵∠C = 2∠B，
∴∠ADC = 2∠B.
∵∠ADC = ∠B + ∠BAD，
∴∠B = ∠BAD，
∴AD = BD = 13，则在Rt△ADE中，根据勾股定理可得$AE = \sqrt{AD^{2} - DE^{2}} = 12$.

17. (2025·唐山古冶区二模)(本小题满分7分)
王老师在数学课上带领同学们做数学游戏，规则如下：

根据游戏规则，回答下面的问题：
(1)若甲报的数为0，则丙报的数是多少？
(2)若甲报了一个整数，丙报出的是正数，则甲报的数最小是多少？

答案： 17.解:
(1)由题意，得$\frac{1}{2} × (0 - 2) - 1 = -2$，
∴丙报的数是-2. 3分
(2)设甲报的数为x.
由题意，得$\frac{1}{2}(x - 2) - 1 ＞ 0$. 5分
解得x ＞ 4.
∵甲报了一个整数，
∴甲报的数最小是5. 7分

18. (2025·江西)(本小题满分8分)
某文物考古研究院用$1:1$复原的青铜蒸馏器进行了蒸馏酒实验.用复原的青铜蒸馏器蒸馏粮食酒和芋头酒，需要的原材料与出酒率（出酒率$=\frac{出酒量}{糟醅量}× 100\%$）如下表：

如果第一次实验分别蒸馏出粮食酒和芋头酒共16公斤；第二次实验分别蒸馏出粮食酒和芋头酒共36公斤，且所用的粮食糟醅量是第一次的2倍，芋头糟醅量是第一次的3倍.
(1)第一次实验分别用了多少公斤粮食糟醅和芋头糟醅？
(2)受限于当时的生产条件，古代青铜蒸馏器的出酒量约为现代复原品的80%.若粮食糟醅中大米占比约为$\frac{1}{4}$，请问，在古代要想蒸馏出这两次实验得到的粮食酒总量，需要准备多少公斤大米？

答案： 18.解:
(1)设第一次实验使用了x公斤粮食糟醅和y公斤芋头糟醅.
由题意，得$\begin{cases} 0.3x + 0.2y = 16, \\ 0.3 × 2x + 0.2 × 3y = 36. \end{cases}$
解得$\begin{cases} x = 40, \\ y = 20. \end{cases}$
答:第一次实验使用了40公斤粮食糟醅和20公斤芋头糟醅. 4分
(2)设需要准备m公斤大米.
$m ÷ \frac{1}{4} × 30\% × 80\% = 30\% × 3 × 40$.
解得m = 37.5.
答:需要准备37.5公斤大米. 8分