《2026年授之以渔河北各地市中考试题汇编数学》

8. (2025·山东烟台)求一组数据方差的算式为：$s^{2}=\frac{1}{n}×[(6-\overline{x})^{2}+(8-\overline{x})^{2}+(8-\overline{x})^{2}+(6-\overline{x})^{2}+(7-\overline{x})^{2}]$，由算式提供的信息，下列说法错误的是 (C)

A.$n$的值是$5$
B.该组数据的平均数是$7$
C.该组数据的众数是$6$
D.若该组数据加入两个数$7$，$7$，则这组新数据的方差变小

答案： 8.C 解析:本题考查方差、众数、平均数.选项A中,这组数据为6,8,8,6,7,
∴n=5,正确;选项B中,平均数$\bar{x}=\frac{6 + 8 + 8 + 6 + 7}{5}=7$，正确;选项C中,数据6和8均出现2次,次数最多,故众数为6和8,而非仅6,错误;选项D中,加入两个7后,平均数不变,数据更集中,方差变小,正确.故选C.

9. (2025·甘肃武威)如图，一个多边形纸片的内角和为$1620^{\circ}$，按图示的剪法剪去一个内角后，所得新多边形的边数为 (A)

A.$12$
B.$11$
C.$10$
D.$9$

答案： 9.A 解析:本题考查多边形的内角和.设原多边形的边数为n,则180°×(n - 2)=1620°,解得n = 11,按题图的剪法剪去一个内角后,新多边形的边数比原多边形的边数多1,为12.故选A.

10. (2025·山东烟台)某商场打折销售一款风扇，若按标价的六折出售，则每台风扇亏损$10$元；若按标价的九折出售，则每台风扇盈利$95$元. 这款风扇每台的标价为 (A)

A.$350$元
B.$320$元
C.$270$元
D.$220$元

答案： 10.A 解析:本题考查一元一次方程的应用.设这款风扇每台的标价为x元,由题意,得0.6x + 10 = 0.9x - 95,解得x = 350,
∴这款风扇每台的标价为350元.故选A.

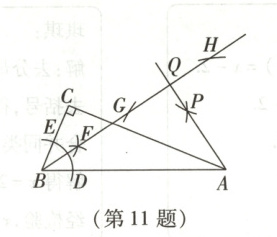
11. (2025·四川遂宁)在$Rt\triangle ABC$中，$\angle C=90^{\circ}$，$AB=13$，$BC=5$，结合尺规作图痕迹提供的信息，求出线段$AQ$的长为 (A)

A.$2\sqrt{13}$
B.$2\sqrt{15}$
C.$6$
D.$\frac{120}{13}$

答案： 11.A 解析:本题考查尺规作图、勾股定理、相似三角形的判定及性质.
∵在Rt△ABC中,∠C = 90°,AB = 13,BC = 5,
∴AC=$\sqrt{13^2 - 5^2}=12$.由作图痕迹可得BG平分∠ABC,即∠CBG = ∠ABG,设BG,AC交于点M,作MN⊥AB于点N,则CM = MN.设CM = MN = x,
∵$S_{\triangle ABC}=S_{\triangle MBC}+S_{\triangle ABM}$，
∴$\frac{1}{2}$BC·AC=$\frac{1}{2}$BC·CM+$\frac{1}{2}$AB·MN,即$\frac{1}{2}$×5×12=$\frac{1}{2}$×5x+$\frac{1}{2}$×13x,解得x=$\frac{10}{3}$，即CM=$\frac{10}{3}$，
∴BM=$\sqrt{5^2 + (\frac{10}{3})^2}=\frac{5\sqrt{13}}{3}$，由作图痕迹可得AQ⊥BH,
∴∠AQB = ∠C = 90°.
∵∠ABG = ∠CBG,
∴△ABQ∼△MBC,
∴$\frac{AQ}{CM}=\frac{AB}{BM}$，即$\frac{AQ}{\frac{10}{3}}=\frac{13}{\frac{5\sqrt{13}}{3}}$，解得AQ = 2$\sqrt{13}$.故选A.

12. (2025·山东东营)如图1，在矩形$ABCD$中，$BC=4$，$E$是$BC$边上的一个动点，$AE\perp EF$，$EF$交$CD$于点$F$，设$BE=x$，$CF=y$，图2是点$E$从点$B$运动到点$C$的过程中，$y$关于$x$的函数图象，则$AB$的长为 (A)

A.$5$
B.$6$
C.$7$
D.$8$

答案： 12.A 解析:本题考查矩形的性质、相似三角形的判定及性质、二次函数的图象和性质.
∵BC = 4,BE = x,
∴CE = BC - BE = 4 - x.
∵矩形ABCD,
∴∠B = ∠C = 90°.
∵AE⊥EF,
∴∠AEB + ∠CEF = 90°.
∵∠CEF + ∠CFE = 90°,
∴∠AEB = ∠CFE,
∴△AEB∼△EFC,
∴$\frac{AB}{CE}=\frac{BE}{CF}$，设AB = m,则$\frac{m}{4 - x}=\frac{x}{y}$，整理得$y=\frac{1}{m}(4x - x^2)$.由题图2可知,该函数图象的顶点坐标为(2,0.8),将(2,0.8)代入$y=\frac{1}{m}(4x - x^2)$，得0.8=$\frac{1}{m}(8 - 4)$，解得m = 5,
∴AB = 5.故选A.