第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
23. (本小题满分11分)
根据素材,完成探究任务:城墙建多高才能抵御进攻方的进攻?
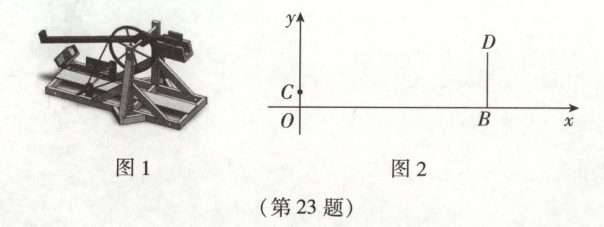
【素材呈现】图1是古代进攻方的一种攻城器械“发石车”.如图2,防守方护城墙BD = 10m,垂直于地面OB,进攻方把“发石车”放置在距B处90m的O处,石块从O处竖直方向上的C处被投出,当石块在空中飞行到与OC的水平距离为50m时,石块离地面OB的最高高度为27m.(注:本题第(2)问不考虑刚好经过点D的情况)
【解决问题】(1)当OC = 2m时.
①参照图2所建立的坐标系,求抛物线(石块运动轨迹)的解析式;
②进攻方的石块能飞进防守方的城墙吗?若能,城墙应加建多高以上,才能让进攻方的石块飞不进防守方城墙;若不能,请说明理由.
(2)石块出发点C与O的距离在什么范围内,防守方无须加高城墙?
根据素材,完成探究任务:城墙建多高才能抵御进攻方的进攻?
【素材呈现】图1是古代进攻方的一种攻城器械“发石车”.如图2,防守方护城墙BD = 10m,垂直于地面OB,进攻方把“发石车”放置在距B处90m的O处,石块从O处竖直方向上的C处被投出,当石块在空中飞行到与OC的水平距离为50m时,石块离地面OB的最高高度为27m.(注:本题第(2)问不考虑刚好经过点D的情况)
【解决问题】(1)当OC = 2m时.
①参照图2所建立的坐标系,求抛物线(石块运动轨迹)的解析式;
②进攻方的石块能飞进防守方的城墙吗?若能,城墙应加建多高以上,才能让进攻方的石块飞不进防守方城墙;若不能,请说明理由.
(2)石块出发点C与O的距离在什么范围内,防守方无须加高城墙?

答案:
23.解:
(1)①
∵OC=2m,
∴C(0,2). 1分
设抛物线的解析式为y=a(x-50)²+27(a≠0).
将C(0,2)代入y=a(x-50)²+27,
得2=a(0-50)²+27.解得a=-$\frac{1}{100}$.
∴y=-$\frac{1}{100}$(x-50)²+27. 4分
②进攻方的石块能飞进防守方的城墙. 5分
∵BD=10m,OB=90m,
∴D(90,10).
令x=90,则y=-$\frac{1}{100}$×(90-50)²+27=11. 7分
∵11>10,
∴进攻方的石块能飞进防守方的城墙. 8分
∵11-10=1(m),
∴城墙应加高1m以上. 9分
(2)设C(0,n).
将C(0,n)代入y=a(x-50)²+27,
得n=a(0-50)²+27,
∴a=$\frac{n-27}{2500}$. 10分
∴抛物线的解析式为y=$\frac{n-27}{2500}$(x-50)²+27.
∴当x=90时,$\frac{n-27}{2500}$(90-50)²+27<10,
解得n<$\frac{7}{16}$.
∴当OC<$\frac{7}{16}$m时,防守方无须加高城墙. 11分
(1)①
∵OC=2m,
∴C(0,2). 1分
设抛物线的解析式为y=a(x-50)²+27(a≠0).
将C(0,2)代入y=a(x-50)²+27,
得2=a(0-50)²+27.解得a=-$\frac{1}{100}$.
∴y=-$\frac{1}{100}$(x-50)²+27. 4分
②进攻方的石块能飞进防守方的城墙. 5分
∵BD=10m,OB=90m,
∴D(90,10).
令x=90,则y=-$\frac{1}{100}$×(90-50)²+27=11. 7分
∵11>10,
∴进攻方的石块能飞进防守方的城墙. 8分
∵11-10=1(m),
∴城墙应加高1m以上. 9分
(2)设C(0,n).
将C(0,n)代入y=a(x-50)²+27,
得n=a(0-50)²+27,
∴a=$\frac{n-27}{2500}$. 10分
∴抛物线的解析式为y=$\frac{n-27}{2500}$(x-50)²+27.
∴当x=90时,$\frac{n-27}{2500}$(90-50)²+27<10,
解得n<$\frac{7}{16}$.
∴当OC<$\frac{7}{16}$m时,防守方无须加高城墙. 11分
查看更多完整答案,请扫码查看


