《2026年授之以渔河北各地市中考试题汇编数学》

20. （本小题满分7分）
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，右图是水平放置的破裂管道有水部分的截面。
（1）请找出截面的圆心$O$；（尺规作图，不写画法，保留作图痕迹）
（2）若这个输水管道有水部分的水面宽$AB = 12cm$，水面最深地方的高度为$4cm$，求这个圆形截面的半径。

答案：
20.
(1)如图1，点O即为所求.3分

(2)如图2，连接OA.由作图可知OD⊥AB，
∴AD = $\frac{1}{2}$AB = 6cm.由题意，得CD = 4cm.设这个圆形截面的半径为rcm，则OD = (r - 4)cm.在Rt△OAD中，$OA^2$ = $OD^2$ + $AD^2$，
∴$r^2$ = $(r - 4)^2$ + $6^2$.6分解得r = 6.5.
答:这个圆形截面的半径是6.5cm.7分

21. （本小题满分9分）
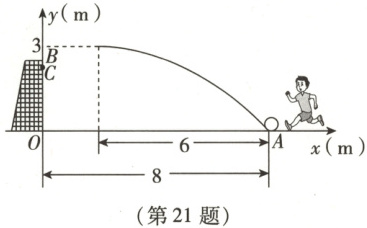
如图，在一次足球训练中，某球员从球门（原点$O$处）正前方$8m$的$A$处射门，球射向球门的路线可近似成一条抛物线，当球飞行的水平距离为$6m$时，球达到最高点，此时球离地面的高度为$3m$。
（1）求抛物线的函数表达式；
（2）已知球门的高$OB$为$2.5m$，通过计算判断该球能否射进球门；（忽略其他因素的影响）
（3）已知点$C$为$OB$上一点，$OC = 2.25m$，若该球员带球向正后方移动$n m$再射门（射门路线的形状、球的最大高度均保持不变），球恰好经过$OC$区域（含点$O$和点$C$），求$n$的取值范围。

答案： 21.解:
(1)
∵8 - 6 = 2(m)，
∴抛物线的顶点坐标为(2，3).设抛物线的函数表达式为y = a$(x - 2)^2$ + 3(a ≠ 0).把点A(8，0)代入，得0 = 36a + 3.解得a = -$\frac{1}{12}$.
∴抛物线的函数表达式为y = -$\frac{1}{12}$$(x - 2)^2$ + 3.4分
(2)当x = 0时，y = -$\frac{1}{12}$×$(-2)^2$ + 3 = $\frac{8}{3}$ ＞ 2.5，
∴该球不能射进球门.6分
(3)由题意得该球员带球向正后方移动nm后，射门路线的表达式为y = -$\frac{1}{12}$$(x - 2 - n)^2$ + 3.把点(0，2.25)代入，得2.25 = -$\frac{1}{12}$$(0 - 2 - n)^2$ + 3.解得n = -5(舍去)或n = 1.把点(0，0)代入，得0 = -$\frac{1}{12}$$(0 - 2 - n)^2$ + 3.解得n = -8(舍去)或n = 4.
∴n的取值范围是1≤n≤4.9分