第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
23. (本小题满分11分)
结合与实践
【情境】要将矩形铁板切割成相同的两部分,焊接成直角护板(如图1),需找到合适的切割线.
【模型】已知矩形ABCD(数据如图2所示). 作一条直线MN,使MN与BC所夹的锐角为45°,且将矩形ABCD分成长度相等的两部分.
【操作】嘉嘉和淇淇尝试用不同方法解决问题.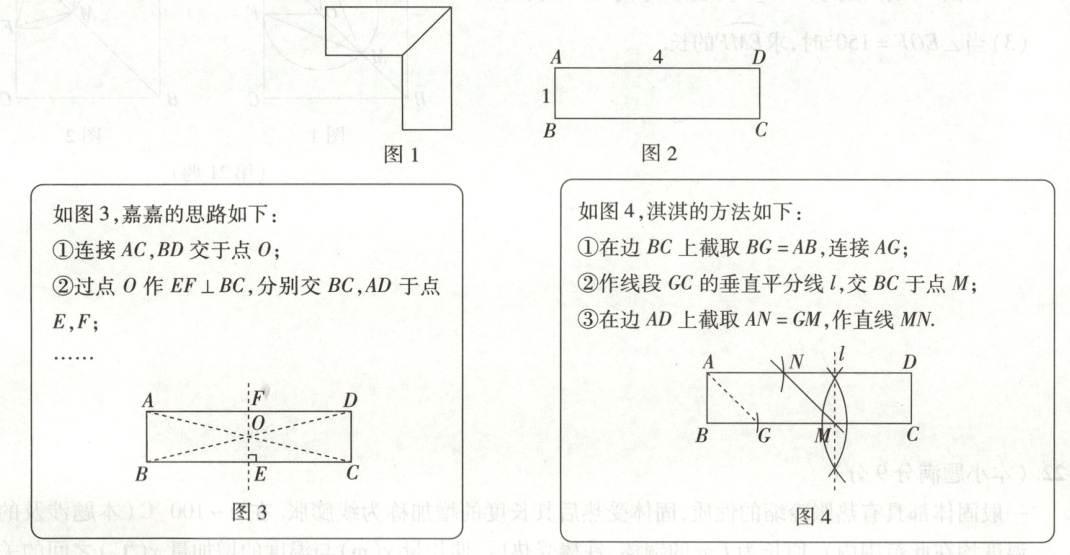
【探究】根据以上描述,解决下列问题.
(1)图2中,矩形ABCD的周长为
(2)在图3的基础上,用尺规作图作出直线MN(作出一条即可,保留作图痕迹,不写作法);
(3)根据淇淇的作图过程,请说明图4中的直线MN符合要求.
【拓展】操作和探究中蕴含着一般性结论,请继续研究下面的问题.
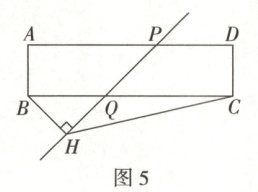
(4)如图5,若直线PQ将矩形ABCD分成长度相等的两部分,分别交边AD,BC于点P,Q,过点B作BH ⊥ PQ于点H,连接CH.
①当∠PQC = 45°时,求tan∠BCH的值;
②当∠BCH最大时,直接写出CH的长.
结合与实践
【情境】要将矩形铁板切割成相同的两部分,焊接成直角护板(如图1),需找到合适的切割线.
【模型】已知矩形ABCD(数据如图2所示). 作一条直线MN,使MN与BC所夹的锐角为45°,且将矩形ABCD分成长度相等的两部分.
【操作】嘉嘉和淇淇尝试用不同方法解决问题.

【探究】根据以上描述,解决下列问题.
(1)图2中,矩形ABCD的周长为
10
;(2)在图3的基础上,用尺规作图作出直线MN(作出一条即可,保留作图痕迹,不写作法);
(3)根据淇淇的作图过程,请说明图4中的直线MN符合要求.
【拓展】操作和探究中蕴含着一般性结论,请继续研究下面的问题.
(4)如图5,若直线PQ将矩形ABCD分成长度相等的两部分,分别交边AD,BC于点P,Q,过点B作BH ⊥ PQ于点H,连接CH.
①当∠PQC = 45°时,求tan∠BCH的值;
②当∠BCH最大时,直接写出CH的长.

答案:
23.解:
(1)10
(2)如图1,直线$MN$即为所求.(答案不唯一)

(3)$\because$四边形$ABCD$是矩形,$AB = 1$,$AD = 4$,$\therefore AD// BC$,$\angle B = 90^{\circ}$,$AB = CD$,$AD = BC$. $\because BG = AB$,$\therefore \angle AGB = 45^{\circ}$. $\because AN = GM$,$AN// GM$,$\therefore$四边形$AGMN$是平行四边形,$\therefore AG// MN$,$\therefore \angle BMN=\angle AGB = 45^{\circ}$. $\because$直线$l$垂直平分$GC$,$\therefore GM = MC$,$\therefore AN = MC$,$\therefore ND + AB + BM = MC + CD + ND$,即直线$MN$将矩形$ABCD$分成周长相等的两部分,$\therefore$直线$MN$符合要求.
(4)①如图2,过点$P$作$PJ \perp BC$于点$J$,则四边形$CDPJ$是矩形,$\therefore PJ = CD = 1$,$PD = JC$. $\because PJ \perp BC$,$\angle PQC = 45^{\circ}$,$\therefore QJ = PJ = 1$. $\because$直线$PQ$将矩形$ABCD$分成周长相等的两部分,$\therefore BQ = PD$,$\therefore BQ = JC=\frac{3}{2}$. $\because BH \perp PQ$,$\angle BQH=\angle PQC = 45^{\circ}$,$\therefore BH = QH$,$\therefore KH = BK = KQ=\frac{1}{2}BQ=\frac{3}{4}$,$\therefore CK=\frac{13}{4}- \frac{3}{4}=\frac{13}{4}-\frac{3}{4}$,$\therefore \tan \angle BCH=\frac{KH}{CK}=\frac{\frac{3}{4}}{\frac{13}{4}}=\frac{3}{13}$.
②$CH = 2\sqrt{2}$.

23.解:
(1)10
(2)如图1,直线$MN$即为所求.(答案不唯一)

(3)$\because$四边形$ABCD$是矩形,$AB = 1$,$AD = 4$,$\therefore AD// BC$,$\angle B = 90^{\circ}$,$AB = CD$,$AD = BC$. $\because BG = AB$,$\therefore \angle AGB = 45^{\circ}$. $\because AN = GM$,$AN// GM$,$\therefore$四边形$AGMN$是平行四边形,$\therefore AG// MN$,$\therefore \angle BMN=\angle AGB = 45^{\circ}$. $\because$直线$l$垂直平分$GC$,$\therefore GM = MC$,$\therefore AN = MC$,$\therefore ND + AB + BM = MC + CD + ND$,即直线$MN$将矩形$ABCD$分成周长相等的两部分,$\therefore$直线$MN$符合要求.
(4)①如图2,过点$P$作$PJ \perp BC$于点$J$,则四边形$CDPJ$是矩形,$\therefore PJ = CD = 1$,$PD = JC$. $\because PJ \perp BC$,$\angle PQC = 45^{\circ}$,$\therefore QJ = PJ = 1$. $\because$直线$PQ$将矩形$ABCD$分成周长相等的两部分,$\therefore BQ = PD$,$\therefore BQ = JC=\frac{3}{2}$. $\because BH \perp PQ$,$\angle BQH=\angle PQC = 45^{\circ}$,$\therefore BH = QH$,$\therefore KH = BK = KQ=\frac{1}{2}BQ=\frac{3}{4}$,$\therefore CK=\frac{13}{4}- \frac{3}{4}=\frac{13}{4}-\frac{3}{4}$,$\therefore \tan \angle BCH=\frac{KH}{CK}=\frac{\frac{3}{4}}{\frac{13}{4}}=\frac{3}{13}$.
②$CH = 2\sqrt{2}$.

查看更多完整答案,请扫码查看


