《2026年授之以渔河北各地市中考试题汇编数学》

23. (2025·内蒙古)（本小题满分11分）
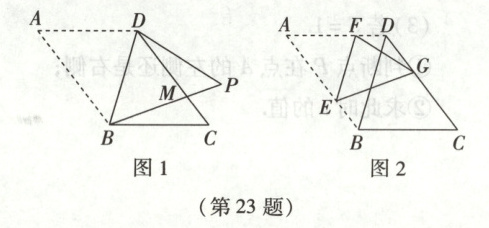
如图，四边形ABCD是一个平行四边形纸片，BD是一条对角线，$BD = BC = 5$，$CD = 6$。
(1)如图1，将平行四边形纸片ABCD沿BD折叠，点A的对应点落在点P处，PB交CD于点M。
①试猜想PM与CM的数量关系，并说明理由；
②求$\triangle BDM$的面积；
(2)如图2，点E，F分别在平行四边形纸片ABCD的AB，AD边上，连接EF，且$EF// BD$，将平行四边形纸片ABCD沿EF折叠，使点A的对应点G落在CD边上，求DG的长。

答案：
23.解:
(1)①PM = CM. 1分 理由:由翻折得AD = DP，∠DAB = ∠DPB.
∵四边形ABCD是平行四边形，
∴AD = BC，∠DAB = ∠BCD.
∴DP = BC，∠DPB = ∠BCD. 又
∵∠DMP = ∠BMC，
∴△DPM≌△BCM(AAS).
∴PM = CM. 3分 ②
∵△DPM≌△BCM，
∴DM = BM. 如图1，过点M作MN⊥BD于点N，过点B作BH⊥CD于点H.
∴$DN = BN = \frac{1}{2}BD = \frac{5}{2}. $
∵BD = BC = 5，CD = 6，
∴$DH = CH = \frac{1}{2}CD = 3. $
∵$cos∠CDB = \frac{DH}{BD} = \frac{3}{5} = \frac{DN}{DM} = \frac{\frac{5}{2}}{DM}，$
∴$DM = \frac{25}{6}. $
∴$MN = \sqrt{DM^2 - DN^2} = \frac{10}{3}. $
∴$S_{\triangle BDM} = \frac{1}{2}BD·MN = \frac{1}{2}×5×\frac{10}{3} = \frac{25}{3} ·s 6$分

(2)如图2，过点C作CP⊥BD于点P，连接AG交BD于点T，过点B作BH⊥CD于点H. 由翻折的性质得AG⊥EF.
∵EF//BD，
∴AG⊥BD. 由
(1)②可得$DH = CH = \frac{1}{2}CD = 3，$
∴$BH = \sqrt{BD^2 - DH^2} = 4. $
∵$S_{\triangle BCD} = \frac{1}{2}CD·BH = \frac{1}{2}BD·CP，$
∴$CP = \frac{CD·BH}{BD} = \frac{24}{5}. $
∴$BP = \sqrt{BC^2 - CP^2} = \frac{7}{5}. $
∴$DP = BD - BP = \frac{18}{5}. 8$分
∵在平行四边形ABCD中，AD = BC，AD//CB，
∴∠ADT = ∠CPB = 90°. 又
∵∠ATD = ∠CPB = 90°，
∴△ADT≌△CBP(AAS).
∴$DT = BP = \frac{7}{5}. $
∵AG⊥BD，CP⊥BD，
∴GT//CP.
∴△DGT∽△DCP.
∵$\frac{DG}{DC} = \frac{DT}{DP}，$即$\frac{DG}{6} = \frac{\frac{7}{5}}{\frac{18}{5}}，$ 解得$DG = \frac{7}{3}. 11$分