《2026年授之以渔河北各地市中考试题汇编数学》

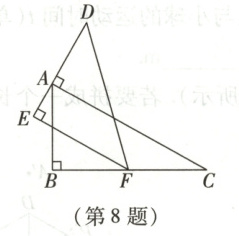
8. 一副三角板按如图所示方式放置，点A在DE上，点F在BC上，AD⊥AC，则∠BFD的度数为（C）

A.45°
B.60°
C.75°
D.80°

答案： 8.C 解析：本题考查平行线的判定及性质。$\because AC \perp DE$，$EF \perp DE$，$\therefore AC // EF$，$\therefore \angle BFE = \angle C = 30^{\circ}$，$\therefore \angle BFD = \angle BFE + \angle DFE = 30^{\circ} + 45^{\circ} = 75^{\circ}$。故选C。

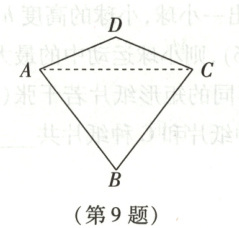
9. 如图，在四边形ABCD中，AB = BC = 6，AD = CD = 4，且点D在△ABC外部，则B，D之间的距离可能是(C)

A.4
B.4.4
C.9
D.11

答案： 9.C 解析：本题考查等腰三角形的性质、勾股定理。假设点D在AC上，连接BD。$\because AB = BC$，$AD = CD$，$\therefore BD \perp AC$，$\therefore BD = \sqrt{AB^{2} - AD^{2}} = 2\sqrt{5}$。假设点A，C重合，则$BD = AB + AD = 10$。$\because$点D在$\triangle ABC$外部，$\therefore 2\sqrt{5} ＜ BD ＜ 10$，$\therefore$B，D之间的距离可能是9。故选C。

10. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中。一房七客多七客，一房九客一房空。”诗中后面两句的意思是：如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间客房。设有客房x间，房客y人，下列方程组中正确的是(A)

A.$\begin{cases}7x + 7 = y, \\ 9(x - 1) = y\end{cases}$
B.$\begin{cases}7x + 7 = y, \\ 9(x + 1) = y\end{cases}$
C.$\begin{cases}7x - 7 = y, \\ 9(x - 1) = y\end{cases}$
D.$\begin{cases}7x - 7 = y, \\ 9(x + 1) = y\end{cases}$

答案： 10.A 解析：本题考查二元一次方程组的应用。由题意，可列方程组为$\begin{cases}7x + 7 = y, \\9(x - 1) = y.\end{cases}$ 故选A。

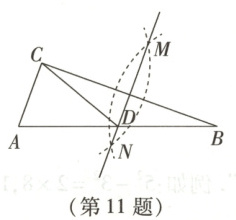
11. 如图，在△ABC中，按以下步骤作图：①分别以点B，C为圆心，大于$\frac{1}{2}BC$的长为半径作弧，两弧相交于点M，N；②作直线MN交AB于点D，连接CD。若CD = AD，∠B = 20°，则下列结论中错误的是(A)

A.∠CAD = 40°
B.∠ACD = 70°
C.点D为△ABC的外心
D.∠ACB = 90°

答案： 11.A 解析：本题考查尺规作图。根据作图痕迹可得MN垂直平分BC，$\therefore CD = BD$，$\therefore \angle BCD = \angle B = 20^{\circ}$。$\because CD = AD$，$\therefore \angle A = \angle ACD$。$\because \angle B + \angle BCD + \angle A + \angle ACD = 180^{\circ}$，$\therefore \angle A = \angle ACD = 70^{\circ}$，$\therefore \angle ACB = 90^{\circ}$，$\therefore$点D为$\triangle ABC$的外心，只有A项错误，符合题意。故选A。

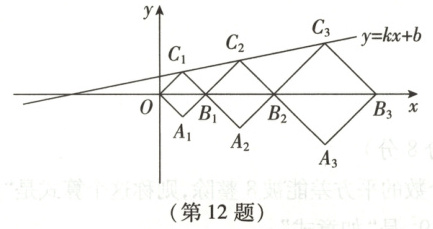
12. 如图，在平面直角坐标系中，正方形OA₁B₁C₁，B₁A₂B₂C₂，B₂A₃B₃C₃，…的顶点B₁，B₂，B₃，…在x轴上，顶点C₁，C₂，C₃，…在直线y = kx + b上，已知OB₁ = 2，B₁B₂ = 3。
①点C₁的坐标为(1，1)；
②直线y = kx + b的表达式为y = $\frac{1}{5}x + \frac{4}{5}$；
③S△C₁B₁C₂∶S△C₂B₂C₃ = 2∶3；
④点Cₙ的横坐标为5·$(\frac{3}{2})^{n - 1} - 4$。
其中说法正确的为(C)

A.①②
B.①②③
C.①②④
D.②③

答案： 12.C 解析：本题考查一次函数与正方形的结合。过点$C_{1}$作$C_{1}D \perp x$轴于点D。$\because$四边形$OA_{1}B_{1}C_{1}$是正方形，$\therefore OC_{1} = B_{1}C_{1}$，$\angle OC_{1}B_{1} = 90^{\circ}$，$\therefore C_{1}D = OD = B_{1}D = \frac{1}{2}OB_{1} = 1$，$\therefore C_{1}(1,1)$，故①正确；同理可得$C_{2}(\frac{7}{2},\frac{3}{2})$，将$C_{1}(1,1)$，$C_{2}(\frac{7}{2},\frac{3}{2})$分别代入$y = kx + b$，得$\begin{cases}k + b = 1, \frac{7}{2}k + b = \frac{3}{2},\end{cases}$ 解得$\begin{cases}k = \frac{1}{5}, \\b = \frac{4}{5},\end{cases}$ $\therefore y = \frac{1}{5}x + \frac{4}{5}$，故 ②正确；根据正方形的性质可得$B_{1}C_{1} = \sqrt{2}$，$B_{2}C_{2} = \frac{3\sqrt{2}}{2}$，$\triangle C_{1}B_{1}C_{2} \backsim \triangle C_{2}B_{2}C_{3}$，$\frac{S_{\triangle C_{1}B_{1}C_{2}}}{S_{\triangle C_{2}B_{2}C_{3}}} = \frac{(B_{1}C_{1})^{2}}{(B_{2}C_{2})^{2}} = \frac{4}{9}$，$\therefore S_{\triangle C_{1}B_{1}C_{2}} : S_{\triangle C_{2}B_{2}C_{3}} = 4 : 9$，故③错误；设$C_{3}(5 + t,t)$，将$C_{3}(5 + t,t)$代入$y = \frac{1}{5}x + \frac{4}{5}$，得$\frac{1}{5}(5 + t) + \frac{4}{5} = t$，解得$t = \frac{9}{4}$，$\therefore$点$C_{3}$的纵坐标为$\frac{9}{4}$。同理可得点$C_{4}$的纵坐标为$\frac{27}{8}$，$·s$，$\therefore$点$C_{n}$的纵坐标为$(\frac{3}{2})^{n - 1}$，$\therefore$点$C_{n}$的横坐标为$5 · (\frac{3}{2})^{n - 1} - 4$，故④正确。综上，说法正确的为①②④。故选C。