2025年更高更妙的高中数学思想与方法高中数学必修第一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年更高更妙的高中数学思想与方法高中数学必修第一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
变式 如图,四棱柱ABCD−A'B'C'D'
是一个无水游泳池,是由一个长方体切掉一
个三棱柱得到的.现在向游泳池内注水,如果
进水速度是均匀的(单位时间内注入的水量
不变),水面与AB的交点为M,则AM的高
度h随时间t变化的图象可能是 ()
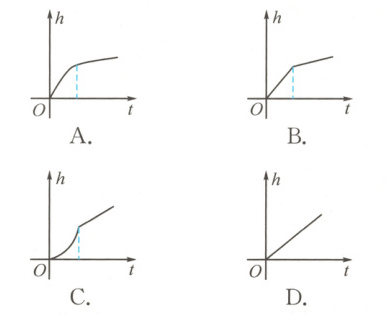

是一个无水游泳池,是由一个长方体切掉一
个三棱柱得到的.现在向游泳池内注水,如果
进水速度是均匀的(单位时间内注入的水量
不变),水面与AB的交点为M,则AM的高
度h随时间t变化的图象可能是 ()


答案:
A
【例 4】已知函数$f(x)=\begin{cases}1+\dfrac{1}{x},x>1, \\x^{2}+1,-1\leqslant x\leqslant1, \\2x+3,x<-1.\end{cases}$
(1)求$f(f(-\dfrac{3}{2}))$;
(2)若$f(a)=1$,求$a$的值.
(1)求$f(f(-\dfrac{3}{2}))$;
(2)若$f(a)=1$,求$a$的值.
答案:
(1) 因为$-\frac{3}{2} < -1$,所以$f(-\frac{3}{2}) = 2×(-\frac{3}{2}) + 3 = 0$。又因为$-1 \leq 0 < 1$,所以$f(f(-\frac{3}{2})) = f(0) = 0^2 + 1 = 1$。
(2) 当$x > 1$时,$f(x) = 1 + \frac{1}{x} > 1$,无解;当$-1 \leq x < 1$时,$f(x) = x^2 + 1 = 1$,解得$x = 0$;当$x < -1$时,$f(x) = 2x + 3 < 1$,无解。综上,$a = 0$。
(1) 因为$-\frac{3}{2} < -1$,所以$f(-\frac{3}{2}) = 2×(-\frac{3}{2}) + 3 = 0$。又因为$-1 \leq 0 < 1$,所以$f(f(-\frac{3}{2})) = f(0) = 0^2 + 1 = 1$。
(2) 当$x > 1$时,$f(x) = 1 + \frac{1}{x} > 1$,无解;当$-1 \leq x < 1$时,$f(x) = x^2 + 1 = 1$,解得$x = 0$;当$x < -1$时,$f(x) = 2x + 3 < 1$,无解。综上,$a = 0$。
[例5]某商场新购进了8台彩电,每台售价3000元,试求销售台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
解析 (1)列表法如下.

(2)图象法如下.
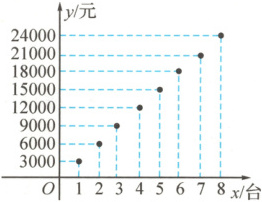
(3)解析式为$y = 3000x(1\leqslant x\leqslant 8,x\in N^{*})$。
解析 (1)列表法如下.

(2)图象法如下.

(3)解析式为$y = 3000x(1\leqslant x\leqslant 8,x\in N^{*})$。
答案:
(1)列表法:
|x/台|1|2|3|4|5|6|7|8|
|---|---|---|---|---|---|---|---|---|
|y/元|3000|6000|9000|12000|15000|18000|21000|24000|
(2)图象法:在平面直角坐标系中,描出点(1,3000),(2,6000),(3,9000),(4,12000),(5,15000),(6,18000),(7,21000),(8,24000)。
(3)解析法:y=3000x(1≤x≤8,x∈N*)
(1)列表法:
|x/台|1|2|3|4|5|6|7|8|
|---|---|---|---|---|---|---|---|---|
|y/元|3000|6000|9000|12000|15000|18000|21000|24000|
(2)图象法:在平面直角坐标系中,描出点(1,3000),(2,6000),(3,9000),(4,12000),(5,15000),(6,18000),(7,21000),(8,24000)。
(3)解析法:y=3000x(1≤x≤8,x∈N*)
查看更多完整答案,请扫码查看


