2025年更高更妙的高中数学思想与方法高中数学必修第一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年更高更妙的高中数学思想与方法高中数学必修第一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
1. 已知$x\gt0$,$y\gt0$,且$x + y = 8$,则$(1 + x)·(1 + y)$的最大值为(
A.$9$
B.$16$
C.$25$
D.$36$
C
)A.$9$
B.$16$
C.$25$
D.$36$
答案:
1. 解析:(方法1)$(1+x)(1+y)=xy+x+y+1=$$xy+9\leqslant \left(\frac{x+y}{2}\right)^{2}+9=25$,当$x=y=4$时取等号,故选C.
(方法2)$10=(x+1)+(y+1)\geqslant 2\sqrt{(x+1)(y+1)}$,解得$(x+1)(y+1)\leqslant 25$,当$x=y=4$时取等号,故选C.
(方法2)$10=(x+1)+(y+1)\geqslant 2\sqrt{(x+1)(y+1)}$,解得$(x+1)(y+1)\leqslant 25$,当$x=y=4$时取等号,故选C.
2. 已知$a\gt0$,$b\gt0$且$ab = 1$,则$\frac{1}{2a}+\frac{1}{2b}+\frac{8}{a + b}$的最小值为(
A.$2$
B.$2\sqrt{2}$
C.$4$
D.$4\sqrt{2}$
C
)A.$2$
B.$2\sqrt{2}$
C.$4$
D.$4\sqrt{2}$
答案:
2. 解析:由基本不等式得$\frac{1}{2a}+\frac{1}{2b}+\frac{8}{a+b}=\frac{a+b}{2}+$$\frac{8}{a+b}\geqslant 4$,当$\begin{cases}a+b=4,\\ab=1\end{cases}$时取等号,故选C.
3. 已知$a\gt0$,$b\gt0$,则$\frac{1}{a}+\frac{1}{b}+2\sqrt{ab}$的最小值为(
A.$2$
B.$2\sqrt{2}$
C.$4$
D.$5$
C
)A.$2$
B.$2\sqrt{2}$
C.$4$
D.$5$
答案:
3. 解析:由均值不等式得$\frac{1}{a}+\frac{1}{b}+2\sqrt{ab}=\frac{a+b}{ab}+$$2\sqrt{ab}\geqslant \frac{2\sqrt{ab}}{ab}+2\sqrt{ab}\geqslant 2\left(\frac{1}{\sqrt{ab}}+\sqrt{ab}\right)\geqslant 4$,当且仅当$\begin{cases}a=b,\\\sqrt{ab}=\frac{1}{\sqrt{ab}},\end{cases}$即$a=b=1$时取等号,故选C.
4. 已知$a\gt0$,$b\gt0$,则下列判断中正确的个数是(
①若$\frac{1}{a}\lt\frac{1}{b}$,则$\sqrt{a}\gt\sqrt{b}$;
②若$a + b = 1$,则$\frac{1}{a}+\frac{4}{b}$的最小值是$10$;
③$\left(a+\frac{1}{a}\right)\left(b+\frac{1}{b}\right)\geq4$;
④函数$y=a+\frac{1}{a + 1}$的最小值为$1$。
A.$1$
B.$2$
C.$3$
D.$4$
B
)①若$\frac{1}{a}\lt\frac{1}{b}$,则$\sqrt{a}\gt\sqrt{b}$;
②若$a + b = 1$,则$\frac{1}{a}+\frac{4}{b}$的最小值是$10$;
③$\left(a+\frac{1}{a}\right)\left(b+\frac{1}{b}\right)\geq4$;
④函数$y=a+\frac{1}{a + 1}$的最小值为$1$。
A.$1$
B.$2$
C.$3$
D.$4$
答案:
4. 解析:对于①,由于$a>0,b>0$,由$\frac{1}{a}<\frac{1}{b}$得$\frac{1}{a}-\frac{1}{b}$$=\frac{b-a}{ab}<0$,则$a>b>0$,故$\sqrt{a}>\sqrt{b}$,所以①正确.
对于②,由于$a>0,b>0$,则$\frac{1}{a}+\frac{4}{b}=\left(\frac{1}{a}+\frac{4}{b}\right)·$$(a+b)=5+\frac{b}{a}+\frac{4a}{b}\geqslant 9$,当且仅当$\begin{cases}a+b=1,\frac{b}{a}=\frac{4a}{b},\end{cases}$即$b$$=2a=\frac{2}{3}$时取等号,故②错误.
对于③,由于$a>0,b>0$,所以$a+\frac{1}{a}\geqslant 2,b+\frac{1}{b}\geqslant$$2$,则$\left(a+\frac{1}{a}\right)\left(b+\frac{1}{b}\right)\geqslant 4$,故③正确.
对于④,由于$a>0,b>0$,所以$y=a+\frac{1}{a+1}=a+1$$+\frac{1}{a+1}-1\geqslant 1$,当且仅当$a+1=\frac{1}{a+1}$,即$a=-2$或$a=0$时取等号,矛盾,所以④错误.
综上所述,判断正确的个数为2,故选B.
对于②,由于$a>0,b>0$,则$\frac{1}{a}+\frac{4}{b}=\left(\frac{1}{a}+\frac{4}{b}\right)·$$(a+b)=5+\frac{b}{a}+\frac{4a}{b}\geqslant 9$,当且仅当$\begin{cases}a+b=1,\frac{b}{a}=\frac{4a}{b},\end{cases}$即$b$$=2a=\frac{2}{3}$时取等号,故②错误.
对于③,由于$a>0,b>0$,所以$a+\frac{1}{a}\geqslant 2,b+\frac{1}{b}\geqslant$$2$,则$\left(a+\frac{1}{a}\right)\left(b+\frac{1}{b}\right)\geqslant 4$,故③正确.
对于④,由于$a>0,b>0$,所以$y=a+\frac{1}{a+1}=a+1$$+\frac{1}{a+1}-1\geqslant 1$,当且仅当$a+1=\frac{1}{a+1}$,即$a=-2$或$a=0$时取等号,矛盾,所以④错误.
综上所述,判断正确的个数为2,故选B.
5. 某市为了加快推进垃圾分类工作,新建了一个垃圾处理厂,
A.$300$吨
B.$400$吨
C.$500$吨
D.$600$吨
每
月最少要处理$300$吨
垃圾,最多要处理$600$吨垃圾,月处理成本(元)与月处理量(吨)之间的
函数关系可近似表示为$y=\frac{1}{2}x^{2}-300x + 80000$,为使每吨的平
均
处理成本最低,该厂每月处理量应为(B
)A.$300$吨
B.$400$吨
C.$500$吨
D.$600$吨
答案:
5. 解析:月处理成本(元)与月处理量(吨)的函数关系为$y=\frac{1}{2}x^{2}-300x+80000$,
所以每吨的平均处理成本为$s=\frac{y}{x}=\frac{\frac{1}{2}x^{2}-300x+80000}{x}$$=\frac{x}{2}+\frac{80000}{x}-300(300\leqslant x\leqslant 600)$.
又$\frac{x}{2}+\frac{80000}{x}-300\geqslant 2\sqrt{\frac{x}{2}· \frac{80000}{x}}-300=100$,当且仅当$\frac{x}{2}=\frac{80000}{x}$时,即$x=400$时,每吨的平均处理成本最低,故选B.
所以每吨的平均处理成本为$s=\frac{y}{x}=\frac{\frac{1}{2}x^{2}-300x+80000}{x}$$=\frac{x}{2}+\frac{80000}{x}-300(300\leqslant x\leqslant 600)$.
又$\frac{x}{2}+\frac{80000}{x}-300\geqslant 2\sqrt{\frac{x}{2}· \frac{80000}{x}}-300=100$,当且仅当$\frac{x}{2}=\frac{80000}{x}$时,即$x=400$时,每吨的平均处理成本最低,故选B.
6. 若正实数$x$,$y$满足$\frac{2}{x}+\frac{1}{y}=1$,且$x + 2y\gt m^{2}+2m$恒成立,则实数$m$的取值范围是(
A.$m\lt-2$或$m\geq4$
B.$m\lt-4$或$m\geq2$
C.$-2\lt m\lt4$
D.$-4\lt m\lt2$
D
)A.$m\lt-2$或$m\geq4$
B.$m\lt-4$或$m\geq2$
C.$-2\lt m\lt4$
D.$-4\lt m\lt2$
答案:
6. 解析:因为正实数$x,y$满足$\frac{2}{x}+\frac{1}{y}=1$,
则$x+2y=(x+2y)\left(\frac{2}{x}+\frac{1}{y}\right)=4+\frac{x}{y}+\frac{4y}{x}\geqslant 8$,
当且仅当$\begin{cases}\frac{2}{x}+\frac{1}{y}=1,\frac{x}{y}=\frac{4y}{x}\end{cases}$即$\begin{cases}x=4,\\y=2\end{cases}$时,$x+2y$取得最小值8,从而只要$m^{2}+2m<8$,即$-4<m<2$时不等式恒成立,故选D.
则$x+2y=(x+2y)\left(\frac{2}{x}+\frac{1}{y}\right)=4+\frac{x}{y}+\frac{4y}{x}\geqslant 8$,
当且仅当$\begin{cases}\frac{2}{x}+\frac{1}{y}=1,\frac{x}{y}=\frac{4y}{x}\end{cases}$即$\begin{cases}x=4,\\y=2\end{cases}$时,$x+2y$取得最小值8,从而只要$m^{2}+2m<8$,即$-4<m<2$时不等式恒成立,故选D.
7. 已知正实数$a$,$b$满足$2(a + b)+\frac{1}{a}+\frac{1}{b}=6$,则$a + b$的取值范围是(
A.$1\leq a + b\leq2$
B.$\frac{1}{2}\leq a + b\leq2$
C.$1\leq a + b\leq4$
D.$a + b\geq4$
A
)A.$1\leq a + b\leq2$
B.$\frac{1}{2}\leq a + b\leq2$
C.$1\leq a + b\leq4$
D.$a + b\geq4$
答案:
7. 解析:由于$6(a+b)=2(a+b)^{2}+(a+b)\left(\frac{1}{a}+\frac{1}{b}\right)=$$2(a+b)^{2}+\frac{b}{a}+\frac{a}{b}+2\geqslant 2(a+b)^{2}+4$,则$(a+b)^{2}$$-3(a+b)+2\leqslant 0$,解得$1\leqslant a+b\leqslant 2$,故选A.
8. 已知正数$x$,$y$满足$\sqrt{4x^{2}-1}+\sqrt{4y^{2}-1}=4xy$,则$9x^{2}+y^{2}$的最小值为(
A.$1$
B.$2$
C.$3$
D.$4$
D
)A.$1$
B.$2$
C.$3$
D.$4$
答案:
8. 解析:由题意知$x,y\geqslant \frac{1}{2}$.
令$\sqrt{4x^{2}-1}=a,\sqrt{4y^{2}-1}=b$,其中$a,b\geqslant 0$,则$x=$$\frac{\sqrt{a^{2}+1}}{2},y=\frac{\sqrt{b^{2}+1}}{2}$,
从而$\sqrt{4x^{2}-1}+\sqrt{4y^{2}-1}=4xy$等价于$a+b=$$\sqrt{(a^{2}+1)(b^{2}+1)}$,等价于$(ab-1)^{2}=0$,即$ab=1$,
所以$\sqrt{4x^{2}-1}· \sqrt{4y^{2}-1}=1$,等价于$16x^{2}y^{2}=$$4x^{2}+4y^{2}$,等价于$\frac{1}{x^{2}}+\frac{1}{y^{2}}=4$,
所以$9x^{2}+y^{2}=\frac{1}{4}\left(\frac{1}{x^{2}}+\frac{1}{y^{2}}\right)(9x^{2}+y^{2})=$$\frac{1}{4}\left(10+\frac{y^{2}}{x^{2}}+\frac{9x^{2}}{y^{2}}\right)\geqslant \frac{1}{4}\left(10+2\sqrt{\frac{y^{2}}{x^{2}}· \frac{9x^{2}}{y^{2}}}\right)=4$,
当且仅当$\begin{cases}\frac{1}{x^{2}}+\frac{1}{y^{2}}=4,\frac{y^{2}}{x^{2}}=\frac{9x^{2}}{y^{2}},\end{cases}$即$\begin{cases}x=\frac{\sqrt{3}}{3},\\y=1\end{cases}$时取等号,
故$9x^{2}+y^{2}$的最小值为4,故选D.
令$\sqrt{4x^{2}-1}=a,\sqrt{4y^{2}-1}=b$,其中$a,b\geqslant 0$,则$x=$$\frac{\sqrt{a^{2}+1}}{2},y=\frac{\sqrt{b^{2}+1}}{2}$,
从而$\sqrt{4x^{2}-1}+\sqrt{4y^{2}-1}=4xy$等价于$a+b=$$\sqrt{(a^{2}+1)(b^{2}+1)}$,等价于$(ab-1)^{2}=0$,即$ab=1$,
所以$\sqrt{4x^{2}-1}· \sqrt{4y^{2}-1}=1$,等价于$16x^{2}y^{2}=$$4x^{2}+4y^{2}$,等价于$\frac{1}{x^{2}}+\frac{1}{y^{2}}=4$,
所以$9x^{2}+y^{2}=\frac{1}{4}\left(\frac{1}{x^{2}}+\frac{1}{y^{2}}\right)(9x^{2}+y^{2})=$$\frac{1}{4}\left(10+\frac{y^{2}}{x^{2}}+\frac{9x^{2}}{y^{2}}\right)\geqslant \frac{1}{4}\left(10+2\sqrt{\frac{y^{2}}{x^{2}}· \frac{9x^{2}}{y^{2}}}\right)=4$,
当且仅当$\begin{cases}\frac{1}{x^{2}}+\frac{1}{y^{2}}=4,\frac{y^{2}}{x^{2}}=\frac{9x^{2}}{y^{2}},\end{cases}$即$\begin{cases}x=\frac{\sqrt{3}}{3},\\y=1\end{cases}$时取等号,
故$9x^{2}+y^{2}$的最小值为4,故选D.
9. 下列说法中正确的有(
A.不等式$a + b\geq2\sqrt{ab}$恒成立
B.存在$a$,使得不等式$a+\frac{1}{a}\leq2$成立
C.若$ab\gt0$,则$\frac{a}{b}+\frac{b}{a}\geq2$
D.若正实数$x$,$y$满足$x + 2y = 1$,则$\frac{2}{x}+\frac{1}{y}\geq8$
BCD
)A.不等式$a + b\geq2\sqrt{ab}$恒成立
B.存在$a$,使得不等式$a+\frac{1}{a}\leq2$成立
C.若$ab\gt0$,则$\frac{a}{b}+\frac{b}{a}\geq2$
D.若正实数$x$,$y$满足$x + 2y = 1$,则$\frac{2}{x}+\frac{1}{y}\geq8$
答案:
9. 解析:不等式$a+b\geqslant 2\sqrt{ab}$恒成立的前提是$a\geqslant 0$,$b\geqslant 0$,故选项A不正确.
当$a$为负数或$a=1$时,不等式$a+\frac{1}{a}\leqslant 2$成立,故选项B正确.
由基本不等式得,$\frac{a}{b}+\frac{b}{a}\geqslant 2\sqrt{\frac{a}{b}· \frac{b}{a}}=2$,故选项C正确.
$\frac{2}{x}+\frac{1}{y}=\left(\frac{2}{x}+\frac{1}{y}\right)(x+2y)=4+\frac{x}{y}+\frac{4y}{x}\geqslant 8$,当且仅当$\begin{cases}x+2y=1,\frac{4y}{x}=\frac{x}{y},\end{cases}$即$\begin{cases}x=\frac{1}{2},\\y=\frac{1}{4}\end{cases}$时取等号,故选项D正确.
故选BCD.
当$a$为负数或$a=1$时,不等式$a+\frac{1}{a}\leqslant 2$成立,故选项B正确.
由基本不等式得,$\frac{a}{b}+\frac{b}{a}\geqslant 2\sqrt{\frac{a}{b}· \frac{b}{a}}=2$,故选项C正确.
$\frac{2}{x}+\frac{1}{y}=\left(\frac{2}{x}+\frac{1}{y}\right)(x+2y)=4+\frac{x}{y}+\frac{4y}{x}\geqslant 8$,当且仅当$\begin{cases}x+2y=1,\frac{4y}{x}=\frac{x}{y},\end{cases}$即$\begin{cases}x=\frac{1}{2},\\y=\frac{1}{4}\end{cases}$时取等号,故选项D正确.
故选BCD.
10. 《九章算术》中有“勾股容方”问题:“今有勾五步,股十二步。问:勾中容方几何?”魏晋时期数学家刘徽在《九章算术注》中利用“出入相补原理”给出了这个问题的一般解法:如图1,用对角线将长和宽分别为$b$和$a$的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青),将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形的长为$a + b$,宽为内接正方形的边长$d$。由刘徽构造的图形可以得到许多重要的结论。
如图3,设$D$为斜边$BC$的中点,作$Rt\triangle ABC$的内接正方形对角线$AE$,过点$A$作$AF\perp BC$于点$F$,则下列推理正确的是(

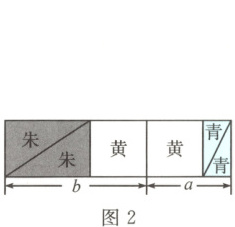
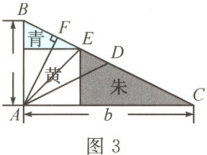
A.由图1和图2的面积相等得$d=\frac{ab}{a + b}$
B.由$AE\geq AF$可得$\sqrt{\frac{a^{2}+b^{2}}{4}}\geq\sqrt{\frac{a + b}{2}}$
C.由$AD\geq AE$可得$\sqrt{\frac{a^{2}+b^{2}}{2}}\geq\frac{2}{\frac{1}{a}+\frac{1}{b}}$
D.由$AD\geq AF$可得$a^{2}+b^{2}\geq a + b$
如图3,设$D$为斜边$BC$的中点,作$Rt\triangle ABC$的内接正方形对角线$AE$,过点$A$作$AF\perp BC$于点$F$,则下列推理正确的是(
AC
)


A.由图1和图2的面积相等得$d=\frac{ab}{a + b}$
B.由$AE\geq AF$可得$\sqrt{\frac{a^{2}+b^{2}}{4}}\geq\sqrt{\frac{a + b}{2}}$
C.由$AD\geq AE$可得$\sqrt{\frac{a^{2}+b^{2}}{2}}\geq\frac{2}{\frac{1}{a}+\frac{1}{b}}$
D.由$AD\geq AF$可得$a^{2}+b^{2}\geq a + b$
答案:
10. 解析:对于选项A,由图1和图2的面积相等得$ab=(a+b)× d$,所以$d=\frac{ab}{a+b}$,故A正确.
对于选项B,因为$AF\perp BC$,所以$\frac{1}{2}× a× b=$$\frac{1}{2}\sqrt{a^{2}+b^{2}}× AF$,所以$AF=\frac{ab}{\sqrt{a^{2}+b^{2}}},AE=\sqrt{2}d$$=\frac{\sqrt{2}ab}{a+b}$.因为$AE\geqslant AF$,所以$\frac{\sqrt{2}ab}{a+b}\geqslant \frac{ab}{\sqrt{a^{2}+b^{2}}}$,整理得$\sqrt{\frac{a^{2}+b^{2}}{2}}\geqslant \frac{a+b}{2}$,故B错误.
对于选项C,因为$D$为斜边$BC$的中点,所以$AD$$=\frac{\sqrt{a^{2}+b^{2}}}{2}$.因为$AD\geqslant AE$,所以$\frac{\sqrt{a^{2}+b^{2}}}{2}\geqslant \frac{\sqrt{2}ab}{a+b}$,整理得$\sqrt{\frac{a^{2}+b^{2}}{2}}\geqslant \frac{2}{\frac{1}{a}+\frac{1}{b}}$,故C正确.
对于选项D,因为$AD\geqslant AF$,所以$\frac{\sqrt{a^{2}+b^{2}}}{2}\geqslant$$\frac{ab}{\sqrt{a^{2}+b^{2}}}$,整理得$a^{2}+b^{2}\geqslant 2ab$,故D错误.
综上,选AC.
对于选项B,因为$AF\perp BC$,所以$\frac{1}{2}× a× b=$$\frac{1}{2}\sqrt{a^{2}+b^{2}}× AF$,所以$AF=\frac{ab}{\sqrt{a^{2}+b^{2}}},AE=\sqrt{2}d$$=\frac{\sqrt{2}ab}{a+b}$.因为$AE\geqslant AF$,所以$\frac{\sqrt{2}ab}{a+b}\geqslant \frac{ab}{\sqrt{a^{2}+b^{2}}}$,整理得$\sqrt{\frac{a^{2}+b^{2}}{2}}\geqslant \frac{a+b}{2}$,故B错误.
对于选项C,因为$D$为斜边$BC$的中点,所以$AD$$=\frac{\sqrt{a^{2}+b^{2}}}{2}$.因为$AD\geqslant AE$,所以$\frac{\sqrt{a^{2}+b^{2}}}{2}\geqslant \frac{\sqrt{2}ab}{a+b}$,整理得$\sqrt{\frac{a^{2}+b^{2}}{2}}\geqslant \frac{2}{\frac{1}{a}+\frac{1}{b}}$,故C正确.
对于选项D,因为$AD\geqslant AF$,所以$\frac{\sqrt{a^{2}+b^{2}}}{2}\geqslant$$\frac{ab}{\sqrt{a^{2}+b^{2}}}$,整理得$a^{2}+b^{2}\geqslant 2ab$,故D错误.
综上,选AC.
查看更多完整答案,请扫码查看


