2025年名校课堂八年级数学上册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校课堂八年级数学上册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 如图所示,已知$∠ABC=∠DCB$,若以“ASA”为依据说明$△ABC≌△DCB$,还需添加的一个条件为
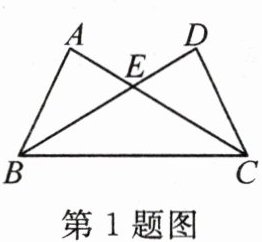
∠ACB=∠DBC
.
答案:
∠ACB=∠DBC
2. 如图,点A,C,D在同一条直线上,$∠B=∠D$,$AB=AD$,$∠BAC=∠DAE$。若$AD=6$,$AE=4$,则$CD=$
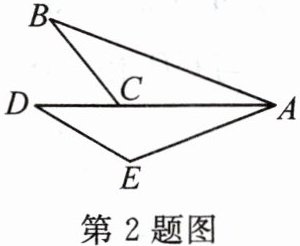
2
.
答案:
2
3. 下列能判定$△ABC≌△DEF$的条件是(
A.$AB=DE$,$BC=EF$,$∠A=∠E$
B.$AB=DE$,$BC=EF$,$∠C=∠E$
C.$∠A=∠E$,$AB=EF$,$∠B=∠D$
D.$∠A=∠D$,$AB=DE$,$∠B=∠E$
D
)A.$AB=DE$,$BC=EF$,$∠A=∠E$
B.$AB=DE$,$BC=EF$,$∠C=∠E$
C.$∠A=∠E$,$AB=EF$,$∠B=∠D$
D.$∠A=∠D$,$AB=DE$,$∠B=∠E$
答案:
D
4. 石家庄外国语校本经典题 如图,已知AB,CD相交于点E,$EC=ED$,$∠C=∠D$。求证:$△AEC≌△BED$。
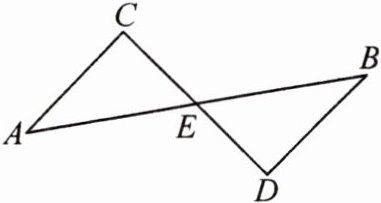

答案:
证明:在△AEC和△BED中,$\begin{cases} ∠C=∠D, \\ CE=ED, \\ ∠AEC=∠BED, \end{cases}$
∴△AEC≌△BED(ASA).
∴△AEC≌△BED(ASA).
5. (2024·合肥瑶海区期末)如图,已知$∠A=∠D$,$AB=DC$,$∠ACE=∠DBF$。求证:$CE=BF$。
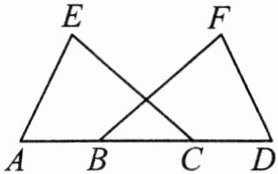

答案:
证明:
∵AB=DC,
∴AB+BC=DC+BC,即AC=DB.在△ACE和△DBF中,$\begin{cases} ∠A=∠D, \\ AC=DB, \end{cases}$
∴△ACE≌△DBF(ASA).
∴CE=BF.∠ACE=∠DBF,
∵AB=DC,
∴AB+BC=DC+BC,即AC=DB.在△ACE和△DBF中,$\begin{cases} ∠A=∠D, \\ AC=DB, \end{cases}$
∴△ACE≌△DBF(ASA).
∴CE=BF.∠ACE=∠DBF,
6. 如图,为了测量点B到河对岸的目标A之间的距离,在与点B同侧的河岸上选择了一点C,测得$∠ABC=65^{\circ}$,$∠ACB=30^{\circ}$,然后在M处立了标杆,使$∠CBM=65^{\circ}$,$∠MCB=30^{\circ}$,测得MB的长是15米,则A,B两点间的距离为(
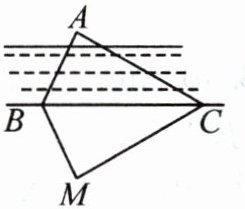
A.10米
B.15米
C.20米
D.30米
B
)
A.10米
B.15米
C.20米
D.30米
答案:
B
7. 北师大附属实验校本经典题(教材P99例4变式)如图,小明站在堤岸的点A处,正对他的点S停有一艘游艇。他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达点C。然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于点D。那么C,D两点间的距离就是在点A处小明与游艇的距离。你知道这是为什么吗?
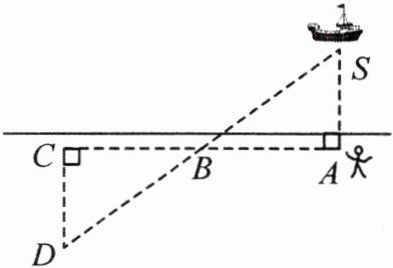

答案:
解:在△ABS和△CBD中,$\begin{cases} ∠A=∠C=90^{\circ}, \\ AB=CB, \\ ∠ABS=∠CBD, \end{cases}$
∴△ABS≌△CBD(ASA).
∴AS=CD.
∴△ABS≌△CBD(ASA).
∴AS=CD.
查看更多完整答案,请扫码查看


