2025年名校课堂八年级数学上册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校课堂八年级数学上册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 下图中全等的三角形有(
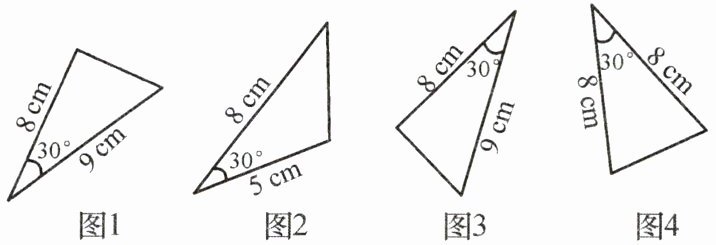
A.图1和图2
B.图2和图3
C.图2和图4
D.图1和图3
D
)
A.图1和图2
B.图2和图3
C.图2和图4
D.图1和图3
答案:
D
2. (2024·六安金安区期末)如图,AC和BD相交于点O,OA=OD.若用“SAS”证明△AOB≌△DOC,则还需添加条件:
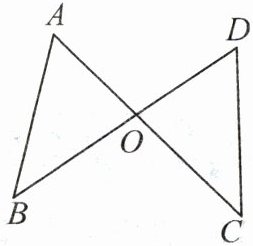
OB=OC
.
答案:
OB=OC
3. 湖南师大附中校本经典题 如图,AB和CD相交于点O,且AO=BO,CO=DO.求证:△AOC≌△BOD.


答案:
证明:在△AOC和△BOD中,$\begin{cases}OA = OB,\\\angle AOC = \angle BOD,\\CO = DO,\end{cases} $
∴△AOC≌△BOD(SAS).
∴△AOC≌△BOD(SAS).
4. (2024·乐山)如图,AB是∠CAD的平分线,AC=AD.求证:∠C=∠D.
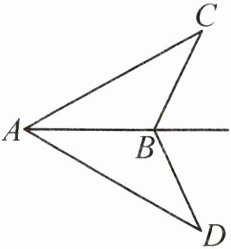

答案:
证明:
∵AB是∠CAD的平分线,
∴∠CAB = ∠DAB.在△ABC和△ABD中,$\begin{cases}AC = AD,\\\angle CAB = \angle DAB,\\AB = AB,\end{cases} $
∴△ABC≌△ABD(SAS).
∴∠C =∠D.
∵AB是∠CAD的平分线,
∴∠CAB = ∠DAB.在△ABC和△ABD中,$\begin{cases}AC = AD,\\\angle CAB = \angle DAB,\\AB = AB,\end{cases} $
∴△ABC≌△ABD(SAS).
∴∠C =∠D.
5. 新考向 情境素材 在生物实验课上,老师布置了“测量锥形瓶底面内径”的任务.小亮同学想到了以下方案:如图,用螺丝钉将两根小棒AD,BC的中点O固定,利用全等三角形的判定及性质,测得C,D之间的距离为10 cm,则可知道内径AB的长度为
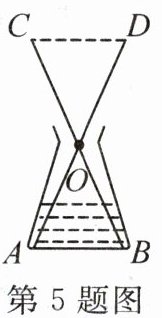
10
cm.
答案:
10
6. 新考向 传统文化 开封风筝是河南开封地区传统民间工艺品.开封风筝历史悠久、种类繁多、做工精细、独具特色.每年农历正月至三月的庙会上,各式各样的风筝竞相牵放,景象十分壮观.如图,这是小华制作的风筝,其中∠EDH=∠FDH,ED=FD,∠EHF=70°,则∠EHD=
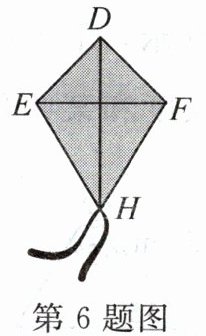
35°
.
答案:
35°
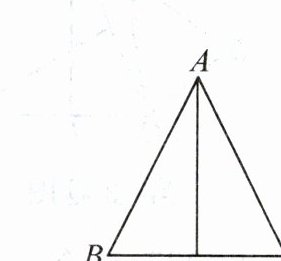
7. 新考向 过程性学习 如图,在△ABC中,AD平分∠BAC,BD=CD,则∠B与∠C相等吗?为什么?
解:相等.理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
$\begin{cases}BD=CD,\\AD=AD,\\∠BAD=∠CAD,\end{cases}$
∴△ABD≌△ACD.
∴∠B=∠C.
以上解答是否正确?若不正确,请说明理由.
解:相等.理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
$\begin{cases}BD=CD,\\AD=AD,\\∠BAD=∠CAD,\end{cases}$
∴△ABD≌△ACD.
∴∠B=∠C.
以上解答是否正确?若不正确,请说明理由.

答案:
解:不正确.理由:错用“SSA”来证明两个三角形全等,∠BAD不是BD与AD的夹角,∠CAD不是CD与AD的夹角.
查看更多完整答案,请扫码查看


