《2025年能力素养与学力提升七年级数学上册人教版》

6. 一根弹簧长$12$ $cm$,在弹性限度(总长不超过$20$ $cm$)内,每挂质量为$1$ $kg$的物体,弹簧伸长$0.5$ $cm$。则代数式$0.5x + 12$表示的实际意义是挂上质量为x kg的物体后,弹簧的总长度。

答案： 挂上质量为x kg的物体后,弹簧的总长度

7. 某新能源汽车销售公司$2022年盈利a$万元,$2022至2024年盈利的年平均增长率为20\%$,则该公司$2024$年的盈利是$a(1+20\%)^{2}$万元。(用含$a$的代数式表示)

答案： $a(1+20\%)^{2}$

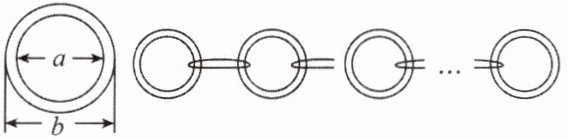
8. 如图,已知圆环内直径为$a$ $cm$,外直径为$b$ $cm$,将$9$个这样的圆环一个接一个环套地连成一条锁链,那么这条锁链拉直后的长度为$(8a+b)cm$。

答案： $(8a+b)cm$

9. 现有两堆棋子,将第一堆中的$3$枚棋子移动到第二堆后,第二堆的棋子数是第一堆棋子的$3$倍。设第一堆原有$m$枚棋子,则第二堆原有$(3m-12)$枚棋子。

答案： $(3m-12)$

10. 甲、乙两地相距$50$ $km$,汽车每小时行驶$v$ $km$,汽车从甲地到乙地需$\frac{50}{v}$ $h$；若汽车每小时加快$3$ $km$,则从甲地到乙地需$\frac{50}{v+3}$ $h$,加快速度后从甲地到乙地可少用$\left(\frac{50}{v}-\frac{50}{v+3}\right)$ $h$。

答案： $\frac{50}{v}$ $\frac{50}{v+3}$ $\left(\frac{50}{v}-\frac{50}{v+3}\right)$

11. 甲、乙两人分别以$a$ $km/h$,$b$ $km/h$的速度,从$A$,$B$两地同时出发,相向而行,$t$ $h$后相遇,则$A$,$B$两地的距离是$(a+b)t$ $km$。

答案： $(a+b)t$

12. 体校里男生人数占学生总数的$60\%$,女生的人数是$a$,这个体校学生总数是$2.5a$人。

答案： $2.5a$

13. 为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多$20$元,如果设每个足球的价格为$x$元,那么用$1500元购进篮球的数量比用800$元购进足球的数量多$\frac{1500}{x+20}-\frac{800}{x}$个。

答案： $\frac{1500}{x}-\frac{800}{x}$

14. 自从有了用字母表示数,我们就可以表达、研究具有更普遍意义的数量关系,有助于我们发现一些有趣的结论,并能解释其中的道理。请根据下列步骤来完成一个有趣的游戏吧！
第一步：从$1到9$中选一个喜欢的数字；
第二步：用这个数乘$5$,再加上$1$；
第三步：将第二步的结果乘$2$,再加上$7$；
第四步：将第三步的结果减去你选择的数。
(1)若你选择的数字是$3$,按以上步骤操作所得的两位数中,个位数字与十位数字的和是9；
(2)再换几个数字按以上步骤操作试试,你会发现所得的两位数中,个位数字与十位数字的和不会发生变化；(填“会”或“不会”)
(3)若选择的数字为$x$,请列出代数式解释(2)中的结论。(要求：不能从$1到9$逐个代入计算)
设选择数字为x,则$(5x+1)×2+7-x=9x+9=10x+9-x$,则所得数字中,十位数字为x,个位数字为$9-x$,$\therefore$个位数字与十位数字的和是$x+9-x=9$.

答案： （1）9 （2）不会 （3）设选择数字为x,则$(5x+1)×2+7-x=9x+9=10x+9-x$,则所得数字中,十位数字为x,个位数字为$9-x$,$\therefore$个位数字与十位数字的和是$x+9-x=9$.