第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
9. 观察以下等式:
第$1$个等式:$\frac{1}{1}+\frac{2}{3}-\frac{1}{3}= \frac{4}{3}$,
第$2$个等式:$\frac{1}{2}+\frac{3}{4}-\frac{1}{8}= \frac{9}{8}$,
第$3$个等式:$\frac{1}{3}+\frac{4}{5}-\frac{1}{15}= \frac{16}{15}$,
第$4$个等式:$\frac{1}{4}+\frac{5}{6}-\frac{1}{24}= \frac{25}{24}$,
第$5$个等式:$\frac{1}{5}+\frac{6}{7}-\frac{1}{35}= \frac{36}{35}$,…
按照以上规律,解决下列问题:
(1)写出第$6$个等式:
(2)写出你猜想的第$n$个等式:
第$1$个等式:$\frac{1}{1}+\frac{2}{3}-\frac{1}{3}= \frac{4}{3}$,
第$2$个等式:$\frac{1}{2}+\frac{3}{4}-\frac{1}{8}= \frac{9}{8}$,
第$3$个等式:$\frac{1}{3}+\frac{4}{5}-\frac{1}{15}= \frac{16}{15}$,
第$4$个等式:$\frac{1}{4}+\frac{5}{6}-\frac{1}{24}= \frac{25}{24}$,
第$5$个等式:$\frac{1}{5}+\frac{6}{7}-\frac{1}{35}= \frac{36}{35}$,…
按照以上规律,解决下列问题:
(1)写出第$6$个等式:
$\frac{1}{6}+\frac{7}{8}-\frac{1}{48}=\frac{49}{48}$
;(2)写出你猜想的第$n$个等式:
$\frac{1}{n}+\frac{n+1}{n+2}-\frac{1}{n(n+2)}=\frac{n(n+2)+1}{n(n+2)}$
(用含$n$的等式表示)。
答案:
(1)$\frac{1}{6}+\frac{7}{8}-\frac{1}{48}=\frac{49}{48}$ (2)$\frac{1}{n}+\frac{n+1}{n+2}-\frac{1}{n(n+2)}=\frac{n(n+2)+1}{n(n+2)}$
10. 甲、乙两人同时同地同向出发,甲每小时走$a$ $km$,乙每小时走$b$ $km$($b > a$),$t$ $h$后两人相距
$t(b-a)$
$km$。
答案:
$t(b-a)$
11. 某快递公司在市区的收费标准为寄一件物品,不超过$1$ $kg付费10$元;超出$1千克的部分加收2$元/ $kg$。乐乐在该公司寄市区内的一件物品,重$x$($x > 1$)$kg$,则需支付
$(2x+8)$
元(用含$x$的代数式表示)。
答案:
$(2x+8)$
12. 一轮船在静水中的航速为$x$ $km/h$,若此轮船在水流速度为$y$ $km/h$的江中航行,则顺流航行的速度是
$(x+y)$
$km/h$,逆流航行的速度是$(x-y)$
$km/h$。若轮船在此江中相距为$s$ $km$的两码头间往返一次,则共需$\left(\frac{s}{x+y}+\frac{s}{x-y}\right)$
$h$。
答案:
$(x+y)$ $(x-y)\left(\frac{s}{x+y}+\frac{s}{x-y}\right)$
1. 有下列五个式子:①$a\cdot2023$;②$\frac{xy + 1}{6}$;③$10÷ a$($a不等于0$);④$1\frac{1}{9}a$;⑤$-n$。其中不符合代数式的书写格式的是(
A.①③⑤
B.②③④
C.①③④
D.②④⑤
C
)A.①③⑤
B.②③④
C.①③④
D.②④⑤
答案:
C
2. 某电子产品原价为$m$,$9$月迎来开学季,商家开展“教育优惠”活动,现售价为$0.8m - 100$,则下列说法中,符合题意的是(
A.原价减$100元后再打8$折
B.原价打$8折后再减100$元
C.原价打$2折后再减100$元
D.原价减$100元后再打2$折
B
)A.原价减$100元后再打8$折
B.原价打$8折后再减100$元
C.原价打$2折后再减100$元
D.原价减$100元后再打2$折
答案:
B
3. 若$x$表示某件物品的原价,则代数式$(1 + 10\%)x$表示的意义是(
A.该物品打九折后的价格
B.该物品价格上涨$10\%$后的售价
C.该物品价格下降$10\%$后的售价
D.该物品价格上涨$10\%$时上涨的价格
B
)A.该物品打九折后的价格
B.该物品价格上涨$10\%$后的售价
C.该物品价格下降$10\%$后的售价
D.该物品价格上涨$10\%$时上涨的价格
答案:
B
4. 下列选项中,能用$2a + 6$表示的是(
A.整条线段的长度
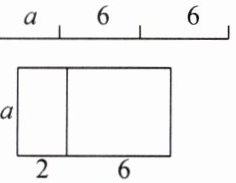
B.整条线段的长度
C.这个长方形的周长
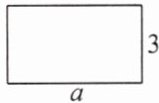
D.这个图形的面积
C
)A.整条线段的长度

B.整条线段的长度
C.这个长方形的周长

D.这个图形的面积
答案:
C
5. 某段公路施工需运送土石方$10^{4}$ $m^{3}$,则土石方日运送量$V$(单位:$m^{3}/$天)与完成运送任务所需时间$t$(单位:天)满足的关系式为
$Vt=10^{4}$或$V=\frac{10^{4}}{t}$
,它们成反比例关系
关系。(填“成正比例”“成反比例”或“不成比例”)
答案:
$Vt=10^{4}$或$V=\frac{10^{4}}{t}$ 反比例关系
查看更多完整答案,请扫码查看


