第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
6. 设$M是-5的相反数与-13$的绝对值的差,$N是比-8$大 6 的数.求$M-N$.
答案:
因为M是-5的相反数与-13的绝对值的差,N是比-8大6的数.所以$M=-(-5)-|-13|=5-13=-8$,$N=-8+6=-2$,所以$M-N=-8-(-2)=-8+2=-6$.
1. 若$a>0$,且$|a|>|b|$,则$a-b$的值是 (
A.正数
B.负数
C.正数或负数
D.0
A
)A.正数
B.负数
C.正数或负数
D.0
答案:
A
2. 已知郝炜同学在计算$35+x$时,误将“$+$”看成“$-$”,结果得 10,则$35+x$的值应为 (
A.20
B.60
C.10
D.70
B
)A.20
B.60
C.10
D.70
答案:
B
3. 有理数$a$,$b$在数轴上的表示如图所示,下列结论:①$a+b<0$;②$a-b<0$;③$a<|b|$;④$-a>-b$;⑤$|a-b|= a-b$.其中正确的有 (
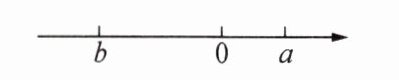
A.2 个
B.3 个
C.4 个
D.5 个
B
)
A.2 个
B.3 个
C.4 个
D.5 个
答案:
B
4. 若$|m|= 5$,$|n|= 3$,$m+n$的绝对值等于它的相反数,则$m-n$的值是 (
A.$-2或-8$
B.$2或-8$
C.$2或8$
D.$-2或8$
A
)A.$-2或-8$
B.$2或-8$
C.$2或8$
D.$-2或8$
答案:
A
5. “数形结合”思想在数轴上得到充分体现,如:在数轴上表示数 5 和$-2的两点之间的距离可列式表示为|5-(-2)|或|-2-5|$;表示数$x和-3的两点之间的距离可列式表示为|x-(-3)|= |x+3|$.那么$|x+3|+|x-2|$的最小值为
5
.
答案:
5
6. 如图是根据幻方改编的“幻圆”游戏,将$-3$,2,$-1$,0,1,$-2$,3,$-4$分别填入图中的圆圈内,使横、竖以及内外两圈上的 4 个数字之和都相等.已知图中$\triangle$、$\odot$分别表示两个数,则$\triangle -\odot$的值为

-4或1
.
答案:
-4或1
7. 小明家购置了一辆续航为 350 km(能行驶的最大路程)的新能源纯电动汽车,他将汽车充满电后连续 7 天每天行车电脑上显示的行驶路程记录如下表(单位:km,以 40 km 为标准,超过部分记为“$+$”,不足部分记为“$-$” ).已知该汽车第三天行驶了 45 km,第六天行驶了 34 km.

(1)“$■$”处的数为
(2)已知小明家这款汽车在行驶结束时,若剩余电量不足续航的 15%,行车电脑就会发出充电提示.请通过计算说明该汽车第七天行驶结束时,行车电脑会不会发出充电提示.

(1)“$■$”处的数为
+5
,“$●$”处的数为 -6
;(2)已知小明家这款汽车在行驶结束时,若剩余电量不足续航的 15%,行车电脑就会发出充电提示.请通过计算说明该汽车第七天行驶结束时,行车电脑会不会发出充电提示.
答案:
(1)+5 -6
(2)由题意,得$-6+2+5-3+8-6+7=2+5+8+7-6-3-6=22-15=7(km)$,$40×7+7=280+7=287(km)$,$350-350×15\%=350-52.5=297.5(km)$,
∵297.5>287,
∴行车电脑会不会发出充电提示.
(1)+5 -6
(2)由题意,得$-6+2+5-3+8-6+7=2+5+8+7-6-3-6=22-15=7(km)$,$40×7+7=280+7=287(km)$,$350-350×15\%=350-52.5=297.5(km)$,
∵297.5>287,
∴行车电脑会不会发出充电提示.
查看更多完整答案,请扫码查看


