《2025年拔尖特训七年级数学上册浙教版》

1. 从甲地到乙地,长途客车原来需要行驶7小时,高速公路开通后,路程缩短了20千米,车速平均每小时增加了40千米,只需要4小时即可到达,则甲、乙两地之间高速公路的路程是(C)
A.320千米
B.380千米
C.400千米
D.420千米

答案： 解：设甲、乙两地之间高速公路的路程是$x$千米，则原来的路程是$(x + 20)$千米。
根据题意，得$\frac{x + 20}{7} + 40 = \frac{x}{4}$
去分母，得$4(x + 20) + 40×28 = 7x$
去括号，得$4x + 80 + 1120 = 7x$
移项、合并同类项，得$-3x = -1200$
系数化为$1$，得$x = 400$
答：甲、乙两地之间高速公路的路程是$400$千米。
C

2. 从一个蓄水池中抽水,甲抽水机单独抽要12小时抽完,乙抽水机单独抽要15小时抽完,丙抽水机单独抽要20小时抽完.若甲、丙先合抽3小时后乙再加入,则距离抽完水还有(A)
A.3小时
B.4小时
C.5小时
D.7小时

答案： 解：设蓄水池的总水量为单位“1”，甲抽水机的工作效率为$\frac{1}{12}$，乙抽水机的工作效率为$\frac{1}{15}$，丙抽水机的工作效率为$\frac{1}{20}$。
设乙加入后还需$x$小时抽完水。
甲、丙先合抽3小时的工作量为：$3×(\frac{1}{12}+\frac{1}{20})$
甲、乙、丙合抽$x$小时的工作量为：$x×(\frac{1}{12}+\frac{1}{15}+\frac{1}{20})$
根据总工作量为1，可列方程：
$3×(\frac{1}{12}+\frac{1}{20}) + x×(\frac{1}{12}+\frac{1}{15}+\frac{1}{20}) = 1$
计算括号内的值：
$\frac{1}{12}+\frac{1}{20}=\frac{5}{60}+\frac{3}{60}=\frac{8}{60}=\frac{2}{15}$
$\frac{1}{12}+\frac{1}{15}+\frac{1}{20}=\frac{5}{60}+\frac{4}{60}+\frac{3}{60}=\frac{12}{60}=\frac{1}{5}$
代入方程得：
$3×\frac{2}{15} + x×\frac{1}{5}=1$
$\frac{6}{15}+\frac{x}{5}=1$
$\frac{2}{5}+\frac{x}{5}=1$
$\frac{x}{5}=1-\frac{2}{5}=\frac{3}{5}$
$x=3$
答：距离抽完水还有3小时，选A。

3. 在一次实践操作中,小丁把两根长为20 cm的竹签绑接成一根35 cm长的竹签,则重叠部分的长度为5cm.

答案： 解：设重叠部分的长度为 $ x $ cm。
根据题意，得 $ 20 + 20 - x = 35 $。
解得 $ x = 5 $。
答：重叠部分的长度为 $ 5 $ cm。

4. 某班有40名学生,会骑车的人数是会游泳人数的3.5倍,两种都会的有8人,两种都不会的有3人,则只会游泳的有2人.

答案： 解：设只会游泳的有$x$人，则会游泳的人数为$(x + 8)$人，会骑车的人数为$3.5(x + 8)$人。
根据全班人数可列方程：$x + 8 + 3.5(x + 8) - 8 + 3 = 40$
化简得：$x + 3.5(x + 8) + 3 = 40$
$x + 3.5x + 28 + 3 = 40$
$4.5x + 31 = 40$
$4.5x = 9$
$x = 2$
答：只会游泳的有$2$人。

5. 在商品市场经常可以听到小贩的叫卖声和顾客的讨价还价声：“10元一个的玩具打八折！”“能不能再便宜2元？”如果小贩真的便宜2元卖了,他还能获利20%,求这个玩具的进价.

答案： 解：设这个玩具的进价为$x$元。
玩具原价10元，打八折后的售价为$10×0.8 = 8$元，再便宜2元后的售价为$8 - 2 = 6$元。
根据售价 = 进价×(1 + 利润率)，可列方程：$x(1 + 20\%)=6$
即$1.2x = 6$
解得$x = 5$
答：这个玩具的进价为5元。

6. 一件商品按进价提高50%后标价,再按标价的八折出售,可获利80元,则其实际售价为(A)
A.480元
B.460元
C.400元
D.200元

答案： 解：设该商品的进价为$x$元。
根据题意，标价为$(1 + 50\%)x = 1.5x$元，实际售价为$0.8×1.5x = 1.2x$元。
因为获利$80$元，所以$1.2x - x = 80$，
解得$0.2x = 80$，$x = 400$。
实际售价为$1.2x = 1.2×400 = 480$元。
答案：A

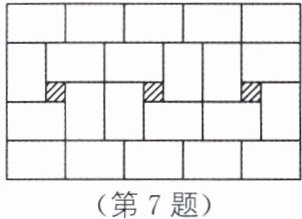
7. 如图,一块展示牌上整齐地贴着许多长方形卡片,这些卡片的大小相同,卡片之间露出了三块正方形空白(图中阴影部分).小明想要配三张正方形图片来填补空白,若卡片的宽是12厘米,则要配边长为8厘米的正方形图片.

答案： 解：设卡片的长为$x$厘米，正方形空白的边长为$y$厘米。
由展示牌横向长度相等可得：$3x = 5×12$，解得$x = 20$。
由卡片长与宽及空白边长关系可得：$x = 12 + y$，即$20 = 12 + y$，解得$y = 8$。
8

8. 某政府准备修建一条公路,若由甲工程队单独修建需3个月完成,每月耗资120万元；若由乙工程队单独修建需6个月完成,每月耗资50万元.现由甲工程队先做一段时间,剩下的由乙工程队单独完成,一共用了4个月完成修建任务,则这样安排共耗资多少万元(时间按整月计算)？

答案： 解：设甲工程队先做$x$个月，则乙工程队做$(4 - x)$个月。
甲工程队的工作效率为$\frac{1}{3}$，乙工程队的工作效率为$\frac{1}{6}$。
根据题意，得$\frac{1}{3}x + \frac{1}{6}(4 - x) = 1$
去分母，得$2x + (4 - x) = 6$
去括号，得$2x + 4 - x = 6$
移项，得$2x - x = 6 - 4$
合并同类项，得$x = 2$
则乙工程队做$4 - 2 = 2$个月。
共耗资：$120×2 + 50×2 = 240 + 100 = 340$（万元）
答：这样安排共耗资340万元。