《2025年拔尖特训七年级数学上册浙教版》

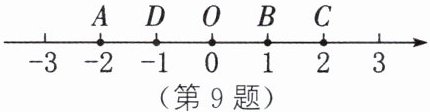
9. 如图,O 为数轴的原点,点 A 表示的数为-2,点 B 表示的数为 1,点 C 表示的数为 2,点 D 表示的数为-1.
(1)数轴可以看成是什么几何图形?
(2)数轴上表示绝对值不大于 2 的部分是什么几何图形？这个几何图形怎样表示？
(3)数轴上表示到原点的距离大于或等于 1 的部分又是什么几何图形？又如何表示这个几何图形？

答案： （1）数轴可以看成规定了原点、正方向和单位长度的直线.
（2）数轴上表示绝对值不大于 2 的部分是线段,这个几何图形表示成线段 AC.
（3）数轴上表示到原点的距离大于或等于 1 的部分是两条射线,这个几何图形表示成射线 DA 和射线 BC.

10. 如图,平面内有六条有公共端点的射线 OA,OB,OC,OD,OE,OF,从射线 OA 开始,按逆时针方向依次在各条射线上写上数 1,2,3,4,5,6,7,…
(1)数 20 在射线OB上.
(2)请写出六条射线上数的排列规律.规律:设 n 为正整数,则数 6n-5 在射线 OA 上;数 6n-4 在射线 OB 上;数 6n-3 在射线 OC 上;数 6n-2 在射线 OD 上;数 6n-1 在射线 OE 上;数 6n 在射线 OF 上.
(3)数 2025 在哪条射线上？因为 2025=6×338-3,所以数 2025 在射线 OC 上.

答案： （1）OB.
（2）规律:设 n 为正整数,则数 6n-5 在射线 OA 上;数 6n-4 在射线 OB 上;数 6n-3 在射线 OC 上;数 6n-2 在射线 OD 上;数 6n-1 在射线 OE 上;数 6n 在射线 OF 上.
（3）因为 2025=6×338-3,所以数 2025 在射线 OC 上.

11. 如图,线段 AB 上的点数与以这些点为端点的线段的总数有如下关系:当线段 AB 上有 3 个点时,线段总共有 3 条;当线段 AB 上有 4 个点时,线段总共有 6 条;当线段 AB 上有 5 个点时,线段总共有 10 条……
(1)当线段 AB 上有 6 个点时,线段总共有15条.
(2)当线段 AB 上有 n 个点时,线段总共有多少条?
根据题意,得当线段 AB 上有 n 个点时,线段总共有$\frac{n(n-1)}{2}$条.
(3)根据上述信息解决问题:
① 某学校七年级共有 20 个班级进行辩论赛,规定进行单循环赛(每两个班级赛一场),那么该校七年级的辩论赛共要进行多少场?
把每个班级看成一个点,则辩论赛共要进行$\frac{20×(20-1)}{2}=190$(场).
② 乘火车从 A 站出发,沿途经过 10 个车站方可到达 B 站,那么在 A,B 两站之间需要设置多少种不同的车票(仅考虑车票的起点站与终点站之分)?
将 12 个车站看成 12 个点,线段共有$\frac{12×11}{2}=66$(条).因为车票有起点站与终点站之分,所以需要设置 2×66=132(种)不同的车票.

答案： （1）15.
（2）根据题意,得当线段 AB 上有 n 个点时,线段总共有$\frac{n(n-1)}{2}$条.
（3）① 把每个班级看成一个点,则辩论赛共要进行$\frac{20×(20-1)}{2}=190$(场).
② 将 12 个车站看成 12 个点,线段共有$\frac{12×11}{2}=66$(条).因为车票有起点站与终点站之分,所以需要设置 2×66=132(种)不同的车票.