《2025年拔尖特训七年级数学上册浙教版》

1. 下列说法中,正确的是 (D)
A.$\sqrt{11}$是有理数
B.11 的平方根是$\sqrt{11}$
C.$\sqrt{11}$不是实数
D.$\sqrt{11}$是无理数

答案： D

2. 如图,数轴上的点 P 表示下列四个无理数中的一个,这个无理数是 (B)
A.$-\sqrt{3}$
B.$\sqrt{3}$
C.$\sqrt{5}$
D.$\pi$

答案： B

3. $-\sqrt{23}$的相反数是$\sqrt{23}$,绝对值为$\sqrt{6}$的数是$\pm \sqrt{6}$.

答案： $\sqrt{23}$ $\pm \sqrt{6}$

4. 把下列各数分别填在相应的横线上(填序号)：
①0,②$-\frac{10}{3}$,③$\sqrt{15}$,④$-|-2|$,⑤$-(-3)$,⑥$-\frac{\pi}{2}$,⑦$\frac{22}{9}$,⑧3.14,⑨$|-4|$,⑩-2.101001…(相邻两个“1”之间依次多一个“0”).
(1)分数：②⑦⑧.
(2)整数：①④⑤⑨.
(3)无理数：③⑥⑩.

答案： （1）②⑦⑧ （2）①④⑤⑨ （3）③⑥⑩

5. 有下列实数：$\sqrt{2}$,-1.5,$\sqrt{5}$,$\pi$,3,将各数与如图所示的数轴上的点对应起来,并把它们按从小到大的顺序排列,用“＜”连接.

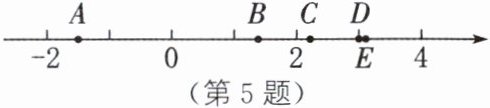
答案： 点 A 表示的数为$-1.5$，点 B 表示的数为$\sqrt{2}$，点 C 表示的数为$\sqrt{5}$，点 D 表示的数为 3，点 E 表示的数为$\pi$.$-1.5＜\sqrt{2}＜\sqrt{5}＜3＜\pi$.

6. 有下列说法：①$\frac{\sqrt{2}}{2}$是分数；②$\frac{\sqrt{2}}{2}$是实数；③$\frac{\sqrt{2}}{2}$是有理数；④$\frac{\sqrt{2}}{2}$是无理数. 其中,正确的有 (B)
A.1个
B.2个
C.3个
D.4个

答案： B

7. 若$\sqrt{3}＜a＜\sqrt{10}$,则下列结论正确的是(B)
A.$1＜a＜3$
B.$1＜a＜4$
C.$2＜a＜3$
D.$2＜a＜4$

答案： B 解析:由$1＜\sqrt{3}＜\sqrt{4}=2$，$3=$$\sqrt{9}＜\sqrt{10}＜4$，可得$1＜a＜4$.

8. 如图,正方形 ABCD 的面积为 5,点 A 在数轴上,且表示的数为 1. 现以点 A 为圆心、AB 长为半径画圆,与数轴相交于点 E(点 E 在点 A 的右边),则点 E 表示的数为 (B)
A.3.2
B.$\sqrt{5}+1$
C.$\sqrt{5}-1$
D.$\sqrt{5}$

答案： B 解析:因为正方形 ABCD 的面积为 5，所以正方形 ABCD 的边长为$\sqrt{5}$.所以点 A，E 之间的距离为$\sqrt{5}$.因为点 A 表示的数是 1，且点 E 在点 A的右边，所以点 E 表示的数为$\sqrt{5}+1$.

9. 如图,数轴上的点 A,B,C,D 中,与表示$-\sqrt{5}$的点距离最近的是 (B)
A.点 A
B.点 B
C.点 C
D.点 D

答案： B 解析:因为$-\sqrt{9}＜-\sqrt{5}＜$$-\sqrt{4}$，即$-3＜-\sqrt{5}＜-2$，所以表示$-\sqrt{5}$的点在点 A 与点 B 之间.又因为$-\sqrt{9}＜-\sqrt{6.25}＜-\sqrt{5}$，所以$-3＜-2.5＜-\sqrt{5}$.所以$-2.5＜$$-\sqrt{5}＜-2$.所以与表示$-\sqrt{5}$的点距离最近的是点 B.

10. 有下列 6 个数：$-100$,$\sqrt{35}$,$10\%$,$\frac{15}{7}$,$-\sqrt{\frac{1}{36}}$,$(-1.5)^3$. 若其中无理数有 x 个,整数有 y 个,负分数有 z 个,则$x+y+z= $4.

答案： 4 解析:$-\sqrt{\frac{1}{36}}=-\frac{1}{6}$.因为在$-100$，$\sqrt{35}$，$10\%$，$\frac{15}{7}$，$-\sqrt{\frac{1}{36}}$，$(-1.5)^3$中，无理数为$\sqrt{35}$，整数为$-100$，负分数为$-\sqrt{\frac{1}{36}}$，$(-1.5)^3$，所以$x=1$，$y=1$，$z=2$.所以$x+y+z=1+1+2=4$.