第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
12. 某防洪大堤所标的警戒水位是37 m,规定在记录每天的水位时,高于警戒水位的部分记为正数,低于警戒水位的部分记为负数.
(1)若夏季某一天的水位为41 m,则应怎么表示?若冬季某一天的水位为32 m,则应怎么表示?
(2)若夏季某一天的水位记为+3.8 m,则实际水位是多少?若冬季某一天的水位记为-1.8 m,则实际水位是多少?
(3)若冬季某一天的水位记为-1.5 m,第二天一场雨后水位上升0.2 m,此时水位应记为多少?实际水位是多少?
(1)若夏季某一天的水位为41 m,则应怎么表示?若冬季某一天的水位为32 m,则应怎么表示?
(2)若夏季某一天的水位记为+3.8 m,则实际水位是多少?若冬季某一天的水位记为-1.8 m,则实际水位是多少?
(3)若冬季某一天的水位记为-1.5 m,第二天一场雨后水位上升0.2 m,此时水位应记为多少?实际水位是多少?
答案:
(1)因为41−37=4(m),所以若夏季某一天的水位为41m,则应记为+4m.因为37−32=5(m),所以若冬季某一天的水位为32m,则应记为−5m.
(2)+3.8m表示高于警戒水位3.8m,37+3.8=40.8(m),即实际水位是40.8m.−1.8m表示低于警戒水位1.8m,37−1.8=35.2(m),即实际水位是35.2m.
(3)−1.5m表示低于警戒水位1.5m,上升0.2m后,仍低于警戒水位1.3m,所以此时水位应记为−1.3m.37−1.3=35.7(m),即实际水位是35.7m.
(1)因为41−37=4(m),所以若夏季某一天的水位为41m,则应记为+4m.因为37−32=5(m),所以若冬季某一天的水位为32m,则应记为−5m.
(2)+3.8m表示高于警戒水位3.8m,37+3.8=40.8(m),即实际水位是40.8m.−1.8m表示低于警戒水位1.8m,37−1.8=35.2(m),即实际水位是35.2m.
(3)−1.5m表示低于警戒水位1.5m,上升0.2m后,仍低于警戒水位1.3m,所以此时水位应记为−1.3m.37−1.3=35.7(m),即实际水位是35.7m.
13. 已知有A,B,C三个数的“家族”:
A:{-1,3.1,-4,6,2.1},
B:{-4.2,2.1,-1,10,$-\frac{1}{8}$},
C:{2.1,-4.2,8,6}.
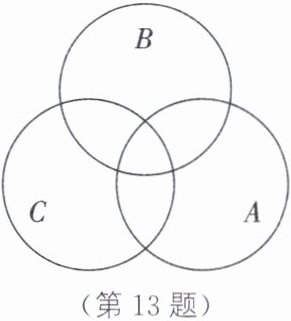
(1)如图,请把每个“家族”中所含的数填入图中的相应部分.
(2)A,B,C三个数的“家族”中的负数有______.
(3)有没有同时属于A,B,C三个数的“家族”的数?若有,请指出.
A:{-1,3.1,-4,6,2.1},
B:{-4.2,2.1,-1,10,$-\frac{1}{8}$},
C:{2.1,-4.2,8,6}.

(1)如图,请把每个“家族”中所含的数填入图中的相应部分.
(2)A,B,C三个数的“家族”中的负数有______.
(3)有没有同时属于A,B,C三个数的“家族”的数?若有,请指出.
答案:
(1)如图所示.
(2)−1,−4,−4.2,−$\frac{1}{8}$.
(3)有.2.1.
(1)如图所示.
(2)−1,−4,−4.2,−$\frac{1}{8}$.
(3)有.2.1.

14. 新考法·阅读理解 阅读材料,并回答问题:
把几个数用大括号括起来,相邻两个数之间用逗号隔开,如{1,2},{1,4,7},…,我们称之为集合,其中的每一个数称为该集合的元素,注意集合中的元素不能重复.
如果一个所有元素均为有理数的集合满足:当有理数x是集合的一个元素时,10-x也必是这个集合 的元素,那么这样的集合我们又称为“黄金集合”. 如集合{0,10}就是一个 “黄金集合”.
(1)集合{1}
(2)请你再写出一个含有两个元素的“黄金集合”,一个含有四个元素的“黄金集合”(不能与上述集合重复).
(3)写出所有“黄金集合"中,元素个数最少的集合
把几个数用大括号括起来,相邻两个数之间用逗号隔开,如{1,2},{1,4,7},…,我们称之为集合,其中的每一个数称为该集合的元素,注意集合中的元素不能重复.
如果一个所有元素均为有理数的集合满足:当有理数x是集合的一个元素时,10-x也必是这个集合 的元素,那么这样的集合我们又称为“黄金集合”. 如集合{0,10}就是一个 “黄金集合”.
(1)集合{1}
不是
“黄金集合”,集合{-1,1} 不是
“黄金集合"(填“是"或 “不是”). (2)请你再写出一个含有两个元素的“黄金集合”,一个含有四个元素的“黄金集合”(不能与上述集合重复).
{1,9};{2,4,6,8}
(3)写出所有“黄金集合"中,元素个数最少的集合
{5}
答案:
(1)不是;不是. 解析:对于集合{1},因为10−1=9,而集合{1}中没有9,所以集合{1}不是“黄金集合”.对于集合{−1,10},因为10−10=0,而集合{−1,10}中没有0,所以集合{−1,10}不是“黄金集合”.
(2)答案不唯一,如因为10−1=9,10−9=1,所以集合{1,9}是“黄金集合”.因为10−2=8,10−4=6,10−6=4,10−8=2,所以集合{2,4,6,8}是“黄金集合”.
(3)因为10−5=5,所以集合{5}是元素个数最少的“黄金集合”.
(1)不是;不是. 解析:对于集合{1},因为10−1=9,而集合{1}中没有9,所以集合{1}不是“黄金集合”.对于集合{−1,10},因为10−10=0,而集合{−1,10}中没有0,所以集合{−1,10}不是“黄金集合”.
(2)答案不唯一,如因为10−1=9,10−9=1,所以集合{1,9}是“黄金集合”.因为10−2=8,10−4=6,10−6=4,10−8=2,所以集合{2,4,6,8}是“黄金集合”.
(3)因为10−5=5,所以集合{5}是元素个数最少的“黄金集合”.
查看更多完整答案,请扫码查看


