《2025年拔尖特训七年级数学上册浙教版》

典例4 (2024·绍兴柯桥期中)在量子物理的研究中,科学家需要精确计算微观粒子的能量.已知某微观粒子的能量E可以用公式$E= \sqrt{a^2+b}$表示.当$a= 2,b= 9$时,该微观粒子的能量E的值在 (A)
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
提示
先计算出当$a= 2,b= 9$时,$\sqrt{a^2+b}$的值,再估算出E的值的大小.

答案： A 解析:当$a=2$，$b=9$时，$E=\sqrt{a^2+b}=\sqrt{2^2+9}=\sqrt{13}$.因为$\sqrt{9}＜\sqrt{13}＜\sqrt{16}$，所以$3＜\sqrt{13}＜4$，即该微观粒子的能量E的值在3和4之间.

[变式] 已知a,b是两个连续整数,且$a＜\sqrt[3]{-16}＜b$,则$2a-3b= $0.

答案： 0 解析:因为$-27＜-16＜-8$，所以$-3＜\sqrt[3]{-16}＜-2$.因为a，b是两个连续整数，$a＜\sqrt[3]{-16}＜b$，所以$a=-3$，$b=-2$.所以$2a-3b=2×(-3)-3×(-2)=-6+6=0$.

典例5 如图,数轴上A,B两点表示的数分别为$\sqrt{2},5.1$,则A,B两点之间表示整数的点共有4个.

答案： 4 解析:因为$1＜2＜4$，所以$1＜\sqrt{2}＜2$.所以A，B两点表示的数之间的整数有2，3，4，5，共4个.

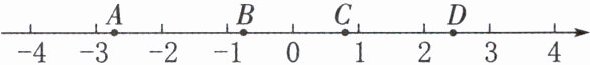
[变式] (2024·绍兴越城期末)如图,实数$\sqrt{2}+1$在数轴上的对应点可能是D.

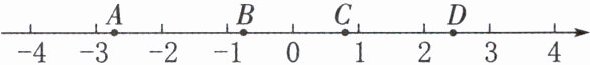
答案： D 解析:因为$\sqrt{1}＜\sqrt{2}＜\sqrt{4}$，所以$1＜\sqrt{2}＜2$.所以$2＜\sqrt{2}+1＜3$.观察数轴上的点可知，则实数$\sqrt{2}+1$在数轴对应的对应点可能是D.

典例6 计算:
(1) $-3^2×2+\sqrt{(-4)^2}+\sqrt[3]{-64}$.
(2) $4×\sqrt{3}-\frac{1}{2}×\sqrt[3]{2}$(结果精确到0.01).

答案： （1）原式$=-9× 2+4-4=-18$.
（2）原式$\approx 4× 1.732-\frac{1}{2}× 1.260=6.928-0.630\approx 6.30$.

[变式] 计算:
(1) $(-2)^3×\frac{1}{8}-\sqrt[3]{27}×(-\sqrt{\frac{1}{9}})$.
(2) $\sqrt{5}+\sqrt[3]{5}-5.022$(结果精确到0.01).

答案： （1）原式$=(-8)× \frac{1}{8}-3×(-\frac{1}{3})=(-1)-(-1)=-1+1=0$.
（2）原式≈2.236+1.710-5.022=-1.076≈-1.08.

典例7 把一个长12cm、宽9cm、高2cm的长方体铁块加工成一个正方体铁块后,其表面积有何变化?试通过计算说明(假设加工过程中无任何损耗).

答案： 由题意可知，加工成的正方体铁块的体积为$12× 9× 2=216(\text{cm}^3)$，所以正方体铁块的棱长为$\sqrt[3]{216}=6(\text{cm})$.因为$6× 6^2=216(\text{cm}^2)$，所以加工后的正方体铁块的表面积为$216\ \text{cm}^2$.又因为$(12× 9+9× 2+12× 2)× 2=300(\text{cm}^2)$，所以原长方体铁块的表面积为$300\ \text{cm}^2$.因为$216＜300$，所以加工成一个正方体铁块后，其表面积变小了.

[变式] 将一个底面半径为10cm的圆柱体容器里的药液倒入一个底面是正方形的长方体容器内,如果药液在两个容器里的高度一样,那么长方体容器的底面边长是______(结果精确到0.1cm).17.7 cm

答案： 17.7 cm 解析:由题意可知，长方体容器的底面积与圆柱体容器的底面积相等，为$\pi× 10^2=100\pi(\text{cm}^2)$，所以长方体容器的底面边长是$\sqrt{100\pi}\approx 17.7(\text{cm})$.