《2025年拔尖特训七年级数学上册浙教版》

14. 已知$A = 2a^{2}b + 3ab^{2}-2$,$B= -6ab^{2}+3a^{2}b + 5$,且$2A + B + C = 0$.
(1)求多项式$C$.
(2)若$a$,$b满足|a + 2| + |b - 1| = 0$,求(1)中多项式$C$的值.

答案：
(1)由题意,得C=-2A-B=-2(2$ a^{2} $b+3a$ b^{2} $-2)-(-6a$ b^{2} $+3$ a^{2} $b+5)=-4$ a^{2} $b-6a$ b^{2} $+4+6a$ b^{2} $-3$ a^{2} $b-5=-7$ a^{2} $b-1.\n
(2)由题意,得a+2=0,b-1=0,所以a=-2,b=1.所以C=-7$ a^{2} $b-1=-7×$ (-2)^{2} $×1-1=-7×4×1-1=-28-1=-29.

15. 某商场一月份的销售额为$a$元,二月份的销售额比一月份的销售额多$b$元,三月份的销售额比二月份的销售额减少10%.
(1)第一季度的总销售额为多少元?
(2)当$a = 20000$,$b = 5000$时,第一季度的总销售额为多少元?

答案：
(1)第一季度的总销售额为a+(a+b)+(a+b)×(1-10%)=(2.9a+1.9b)元$.\n(2)$当a=20000,b=5000时,2.9a+1.9b=2.9×20000+1.9×5000=67500.所以第一季度的总销售额为67500元.

16. 按照如图所示的步骤计算并回答问题：

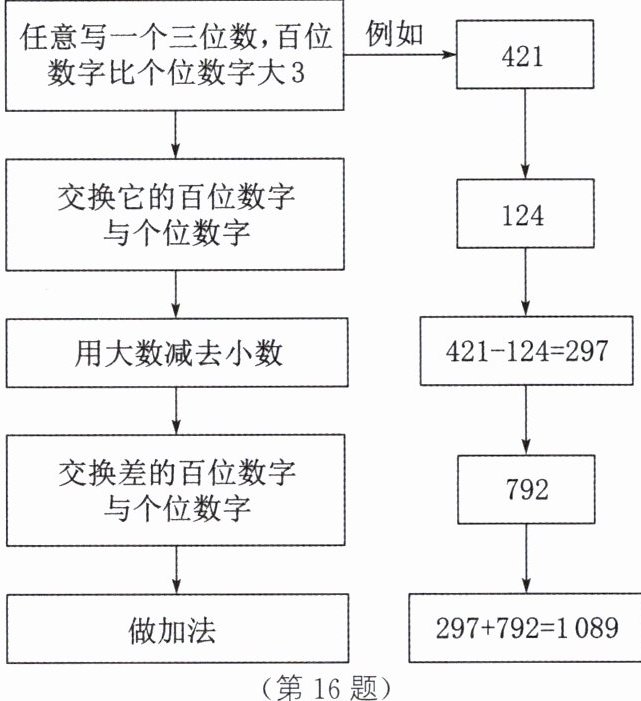
(1)尝试用不同的三位数再做几次,结果都是1089吗?
(2)请你运用所学的整式的知识解释其中的道理.

答案：
(1)具体尝试过程略,用不同的三位数再做几次,结果都是$1089.\n(2)$设这个三位数为100(3+c)+10b+c,交换百位数字与个位数字后这个三位数变为100c+10b+3+c.根据题意,得[100(3+c)+10b+c]-(100c+10b+3+c)=297.交换297的百位数字和个位数字得到792,而297+792=1089,所以用不同的三位数再做几次,结果都是1089.