《2025年拔尖特训七年级数学上册浙教版》

1. 下列式子中,属于单项式的为 (B)
A.8(xy+5)
B.π
C.$\frac{a+1}{2}$
D.$\frac{y}{x}$

答案： B

2. 下列说法中,正确的是 (D)
A.$-\frac{2vt}{3}$的系数是 2
B.$3^{2}a^{3}b^{4}$的次数是 9
C.$3x^{2}-x-5$的常数项是 5
D.$x^{3}+2x^{2}-x-2$是三次多项式

答案： D 解析：$-\frac{2vt}{3}$的系数是$-\frac{2}{3}$，故A选项的说法错误；$3^{2}a^{3}b^{4}$的次数是$3+4=7$，故B选项的说法错误；$3x^{2}-x-5$的常数项是$-5$，故C选项的说法错误；多项式$x^{3}+2x^{2}-x-2$的次数为3，为三次多项式，故D选项的说法正确.

3. 在代数式$\sqrt{2},a^{2}-b^{2},\frac{x-2y}{x},\sqrt{3x},\frac{1}{a}+b$中,属于整式的有2个.

答案： 2

4. 已知小李有$a^{2}$本书,小张给了小李 m 本后,他们两人的书就一样多,则小张原来有$(a^{2}+2m)$本书,这是一个二次二项式.

答案： $(a^{2}+2m)$ 二 二

5. 小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同).

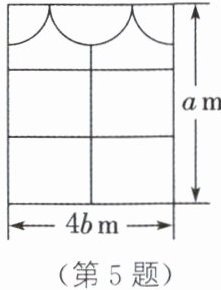
(1) 装饰物所占的面积是多少? 窗户中能射进阳光的部分的面积是多少(窗框的面积忽略不计)?
(2) 观察(1)中所得到的结果,它们是单项式还是多项式? 次数分别是多少?

答案： （1）由题意知，四分之一圆与半圆的半径均为$\frac{4b}{4}=b(\text{m})$，所以装饰物所占的面积是$\pi b^{2}\ \text{m}^{2}$，窗户中能射进阳光的部分的面积是$(4ab-\pi b^{2})\text{m}^{2}$.
（2）$\pi b^{2}$是单项式，次数是2；$4ab-\pi b^{2}$是多项式，次数是2.

6. 已知单项式$\frac{1}{2}x^{4-m}y与6xy^{2}$的次数相同,则 m 的值为 (B)
A.1
B.2
C.3
D.4

答案： B 解析：因为单项式$\frac{1}{2}x^{4-m}y$与$6xy^{2}$的次数相同，所以$4-m+1=1+2$，即$5-m=3$，解得$m=2$.

7. 若$5x^{4}y^{n}+(m-2)x-1$是关于 x,y 的六次三项式,则下列说法中,错误的是 (A)
A.m 可以是任意数
B.六次项是$5x^{4}y^{n}$
C.n= 2
D.常数项是-1

答案： A 解析：因为$5x^{4}y^{n}+(m-2)x-1$是关于$x$，$y$的六次三项式，所以六次项是$5x^{4}y^{n}$，常数项是$-1$.所以$n+4=6$，$m-2\neq0$，则$n=2$，$m\neq2$.所以选项A错误，符合题意.

8. 同时含有字母 a,b,c 且系数为 1 的六次单项式按以下规则排序:先比较 a 的次数,a 的次数高的单项式排在前面,若 a 的次数相同,再比较 b 的次数,最后比较 c 的次数,均是先高次后低次,则$a^{2}b^{3}c$排在 (A)
A.第4位
B.第5位
C.第6位
D.第7位

答案： A 解析：由题意，可依次排为$a^{4}bc$，$a^{3}b^{2}c$，$a^{3}bc^{2}$，$a^{2}b^{3}c$，…，所以$a^{2}b^{3}c$排在第4位.

9. 若一个多项式的各项的次数都相同,则这个多项式叫作齐次多项式,例如:$x^{3}+3xy^{2}+4xyz+2y^{3}$是三次齐次多项式.若$a^{x+3}b^{2}-6ab^{3}c^{2}$是齐次多项式,则 x 的值为 (C)
A.-1
B.0
C.1
D.2

答案： C 解析：由题意，得$x+3+2=1+3+2$，解得$x=1$.

10. (2023·金华期末)观察下列一组单项式$:x,-2x^2,4x^3,-8x^4,16x^5,… $根据你发现的规律可知,第7个单项式为$64x^{7}$.

答案： $64x^{7}$

11. 易错题 已知一个整式具备下列条件:① 它是一个关于 x 的二次三项式;② 各项系数的和等于 10;③ 它的二次项系数和常数项都比-2 小 1. 请写出满足这些条件的整式:$-3x^{2}+16x-3$.

答案： $-3x^{2}+16x-3$ 解析：根据题意可知，它的二次项系数和常数项都比$-2$小1，即二次项系数是$-3$，常数项是$-3$.因为各项系数的和等于10，所以一次项系数是$10-(-3)-(-3)=16$.所以满足这些条件的整式为$-3x^{2}+16x-3$.

12. 根据题意列出代数式,并判断是否为整式.若是整式,则说明是单项式还是多项式.
(1) 某商店以七五折的优惠销售商品,则定价是 x 元的商品的售价是多少元?
(2) 一列火车从 A 站开往 B 站,火车的速度是 a 千米/时,A,B 两站间的距离是 120 千米,则火车从 A 站开到 B 站需要多长时间?
(3) 某单位原有工作人员 m 人,现精简机构,减少 25%的工作人员后又引进人才 3 人,则该单位现有工作人员多少人?

答案： （1）售价是$0.75x$元，$0.75x$是整式，是单项式.
（2）需要$\frac{120}{a}$小时，$\frac{120}{a}$不是整式.
（3）现有工作人员$[(1-25\%)m+3]$人，$(1-25\%)m+3$是整式，是多项式.