《2025年拔尖特训七年级数学上册浙教版》

1. (2023·孝感云梦期末)若“!”是一种数学运算符号,且1!= 1,2!= 2×1= 2,3!= 3×2×1= 6,4!= 4×3×2×1= 24,…,则$\frac{100!}{98!}$的值为 (C)
A.$\frac{50}{49}$
B.99!
C.9900
D.2!

答案： C 解析:由题意,得100! =100×99×…×3×2×1,98! =98×97×…×3×2×1，所以$\frac{100!}{98!}=\frac{100×99×…×3×2×1}{98×97×…×3×2×1}=100×99=9900.$

2. 对于整数a,b,规定一种新的运算“▽”,即a▽b表示从a开始的连续|b|个整数的积,如2▽3= 2×3×4= 24,(-5)▽(-2)= (-5)×(-4)= 20,则(-7)▽[1▽(-2)]的值为 (C)
A.-210
B.-42
C.42
D.56

答案： C 解析:$(-7)\nabla [1\nabla (-2)]=(-7)\nabla (1×2)=(-7)\nabla 2=(-7)×(-6)=42.$

3. (2024·甘肃)定义一种新运算“*”,规定运算法则为m*n= $m^n$-mn(m,n均为整数,且m≠0).例如:2*3= $2^3$-2×3= 2,则(-2)*2= 8.

答案： 8 解析:$(-2)*2=(-2)^{2}-(-2)×2=4+4=8.$

4. 新定义一种运算“△”:a△b= $\frac{1}{a}÷(-\frac{2}{b})$,则(-3△4)△2的值是$-\frac{3}{2}$.

答案： $-\frac{3}{2}$ 解析:因为$a△b=\frac{1}{a}÷(-\frac{2}{b})$,所以$(-3△4)△2=[-\frac{1}{3}÷(-\frac{2}{4})]△2=\frac{2}{3}△2=\frac{3}{2}÷(-\frac{2}{2})=-\frac{3}{2}.$

5. 对于有理数a,b,定义一种新的运算:a⊗b= ab-a+b.例如:1⊗2= 1×2-1+2.求:
(1)(-3)⊗4的值.
(2)[5⊗(-2)]⊗3的值.

答案： （1）由题意,可得$(-3)\otimes 4=(-3)×4-(-3)+4=-12+3+4=-5.$
（2）由题意,可得$[5\otimes (-2)]\otimes 3=[5×(-2)-5+(-2)]\otimes 3=(-10-5-2)\otimes 3=(-17)\otimes 3=(-17)×3-(-17)+3=-51+17+3=-31.$

6. 定义一种新运算“*”:a*b= (a+1)(b+1),等号的右侧为通常的混合运算.
(1)计算(-3)*(-2)与(-2)*(-3),此运算满足交换律吗?
(2)计算[(-4)*(-3)]*(-2)与(-4)*[(-3)*(-2)],此运算满足结合律吗?

答案： （1）$(-3)*(-2)=(-3+1)×(-2+1)=(-2)×(-1)=2,$$(-2)*(-3)=(-2+1)×(-3+1)=(-1)×(-2)=2,$所以$(-3)*(-2)=(-2)*(-3),$此运算满足交换律.
（2）$[(-4)*(-3)]*(-2)=[(-4+1)×(-3+1)]*(-2)=6*(-2)=(6+1)×(-2+1)=-7,$$(-4)*[(-3)*(-2)]=(-4)*[(-3+1)×(-2+1)]=(-4)*2=(-4+1)×(2+1)=(-3)×3=-9,$所以$[(-4)*(-3)]*(-2)≠(-4)*[(-3)*(-2)]$,此运算不满足结合律.

7. 若“三角”表示运算:a-b+c,“方框”表示运算:x-y+z+w,求×的值.

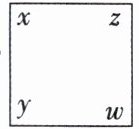
答案： 根据题意,得原式$=(\frac{1}{4}-\frac{1}{2}+\frac{1}{6})×(-2-1.5+1.5-6)=(\frac{1}{4}-\frac{1}{2}+\frac{1}{6})×(-8)=\frac{1}{4}×(-8)-\frac{1}{2}×(-8)+\frac{1}{6}×(-8)=-2+4-\frac{4}{3}=\frac{2}{3}.$

8. 若a是不为2的有理数,则我们把$\frac{2}{2-a}$称为a的“奇特数”.例如:4的“奇特数”是$\frac{2}{2-4}= -1$,-1的“奇特数”是$\frac{2}{2-(-1)}= \frac{2}{3}$.已知$a_1$= 4,$a_2是a_1$的“奇特数”,$a_3是a_2$的“奇特数”,$a_4是a_3$的“奇特数”,…,以此类推,$a_{2024}$的值为 (D)
A.4
B.-1
C.$\frac{2}{3}$
D.$\frac{3}{2}$

答案： D 解析:因为$a_{1}=4$,所以由"奇特数"的定义,得$a_{2}=\frac{2}{2-4}=-1,a_{3}=\frac{2}{2-(-1)}=\frac{2}{3},a_{4}=\frac{2}{2-\frac{2}{3}}=\frac{3}{2},a_{5}=\frac{2}{2-\frac{3}{2}}=4,...$.由此可以发现,这些数以$4,-1,\frac{2}{3},\frac{3}{2}$为一组循环出现.因为$2024÷4=506$,所以$a_{2024}=a_{4}=\frac{3}{2}.$