《2025年拔尖特训七年级数学上册浙教版》

9. 阅读材料,并回答下列问题:
式子1+2+3+4+5+…+100表示从1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便,我们可以将1+2+3+4+5+…+100表示为$\sum_{n= 1}^{100}n$.这里的“∑”是求和符号,如1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和可表示为$\sum_{n= 1}^{50}(2n-1)$,又如$1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3+10^3可表示为\sum_{n= 1}^{10}n^3$.
(1)式子2+4+6+8+10+…+100(即从2开始的不超过100的连续偶数的和)用求和符号可以怎样表示?
(2)式子$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{10}$用求和符号可以怎样表示?
(3)计算:$\sum_{n= 1}^{6}(n^2-1)$.

答案： （1）根据题意,得$2+4+6+8+10+…+100=\sum\limits_{n=1}^{50}2n.$
（2）$1+\frac{1}{2}+\frac{1}{3}+... +\frac{1}{10}=\sum\limits_{n=1}^{10}\frac{1}{n}.$
（3）原式$=(1-1)+(4-1)+(9-1)+(16-1)+(25-1)+(36-1)=85.$

10. 新考向·数学文化 如图,第十四届国际数学教育大会(简称ICME-14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的灿烂文明,图案中右下方的图形是用我国古代的计数符号写出的八进制中的3745.我们常用的数是十进制数,如4657= 4×$10^3$+6×$10^2$+5×$10^1$+7×1,在电子计算机中用的二进制,如二进制中的110= 1×$2^2$+1×$2^1$+0×1等于十进制中的数6,则八进制中的3745换算成十进制是 2021.
]

答案： 2021 解析:因为$3×8^{3}+7×8^{2}+4×8^{1}+5×1=1536+448+32+5=2021$,所以八进制中的 3745 换算成十进制是 2021.

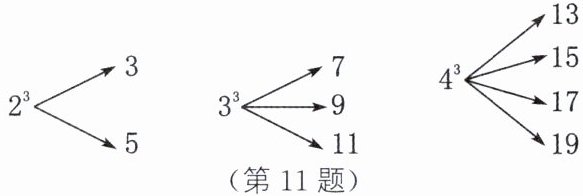
11. 一个自然数的立方可以分裂成若干个连续奇数的和,如$2^3$,$3^3和4^3$分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即$2^3$= 3+5,$3^3$= 7+9+11,$4^3$= 13+15+17+19.若$6^3$也按照此规律来进行“分裂”,则$6^3$“分裂”出的奇数中,最大的奇数是多少?
]

答案： 因为$2^{3}=3+5$，"分裂"出的第一个数是$3,3=2×1+1,$$3^{3}=7+9+11$，"分裂"出的第一个数是$7,7=3×2+1,$$4^{3}=13+15+17+19$，"分裂"出的第一个数是$13,13=4×3+1,... ,$所以$n^{3}$"分裂"出的第一个数是$n(n-1)+1.$所以$6^{3}$"分裂"出的第一个数是$6×5+1=31.$所以易得$6^{3}$"分裂"出的奇数中,最大的奇数是$31+2×(6-1)=41.$