《2025年拔尖特训七年级数学上册浙教版》

1. 若$x= -1,y= 4$,则代数式$2(x+y)$的值为(C)
A.-6
B.-10
C.6
D.2

答案： C

2. 当$x= 2$时,代数式$ax-2$的值为4,则$a$的值为(C)
A.-1
B.0
C.3
D.1

答案： C 解析:因为当x=2时,代数式ax-2的值为4,所以2a-2=4.所以a=3.

3. 已知$x-2y= -3$,则$4(x-2y)^{2}-3(x-2y)+20$的值是65.

答案： 65 解析:因为x-2y=-3,所以原式=4×(-3)²-3×(-3)+20=36+9+20=65.

4. 当$a= \frac{1}{2},b= -\frac{5}{2}$时,求下列代数式的值.
(1)$(a+b)^{2}-(a-b)^{2}$.
(2)$a^{2}+2ab+b^{2}$.

答案：
(1)当a= $\frac{1}{2}$,b=-$\frac{5}{2}$时,原式=($\frac{1}{2}$-$\frac{5}{2}$)²-[$\frac{1}{2}$-(-$\frac{5}{2}$)]²=4-9=-5.
(2)当a= $\frac{1}{2}$,b=-$\frac{5}{2}$时,原式=($\frac{1}{2}$)² + 2×$\frac{1}{2}$×(-$\frac{5}{2}$)+(-$\frac{5}{2}$)²=$\frac{1}{4}$-$\frac{5}{2}$+$\frac{25}{4}$=4.

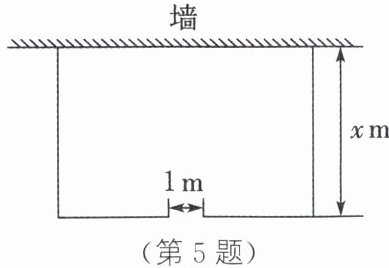
5. 有一长为20 m的篱笆,利用它和房屋的一面墙围成如图所示的园子,园子的宽为$x$ m,园子开了一扇门,门的宽度为1 m.
(1)用含$x$的代数式表示园子的面积.
(2)当$x= 5$时,求园子的面积.

答案：
(1)由题意,得园子的面积为(20-2x+1)x=(21-2x)x m².
(2)当x=5时,(21-2x)x=(21-2×5)×5=11×5=55.所以园子的面积是55 m².

6. 当$a= 5$时,下列代数式的值最大的是(D)
A.$2a+3$
B.$\frac{a}{2}-1$
C.$\frac{1}{5}a^{2}-2a+10$
D.$\frac{7a^{2}-100}{5}$

答案： D 解析:当a=5时,2a+3=13,$\frac{a}{2}$-1=$\frac{3}{2}$,$\frac{1}{5}$a²-2a+10=$\frac{1}{5}$×5²-2×5+10=5,$\frac{7a²-100}{5}$=$\frac{7×5²-100}{5}$=15.故选项D中的代数式的值最大.

7. ★按如图所示的程序,若输入$x$的值为4,则输出的结果是(B)
A.1750
B.1540
C.1950
D.2020

答案： B 解析:把x=4代入$\frac{x(x+1)}{2}$,得$\frac{4×(4+1)}{2}$=10,10＜100;把x=10代入$\frac{x(x+1)}{2}$,得$\frac{10×(10+1)}{2}$=55,55＜100;把x=55代入$\frac{x(x+1)}{2}$,得$\frac{55×(55+1)}{2}$=1540,1540＞100.故最后输出的结果是1540.

8. 在公园内,牡丹按正方形种植,在它的周围种植芍药,如图所示的图形反映了牡丹的列数$n$和芍药的数量之间的关系.当$n= 15$时,芍药的数量为(C)
A.80株
B.100株
C.120株
D.140株

答案： C 解析:设芍药的数量为x株.根据题意,得当n=1时,x=8;当n=2时,x=16;当n=3时,x=24;当n=4时,x=32……由此可得,x=8n.所以当n=15时,芍药的数量为15×8=120(株).

9. 若$x= m$,代数式$x^{2}-x-1$的值为2,则代数式$m^{2}-m+2022$的值为2025.

答案： 2025 解析:因为当x=m时,代数式x²-x-1的值为2,所以m²-m-1=2,即m²-m=3.所以m²-m+2022=3+2022=2025.

10. 若$|a|= 1,b^{2}= 4$,且$a＞b$,则代数式$3a-2b$的值是7或1.

答案： 7或1 解析:因为|a|=1,b²=4,且a＞b,所以a=±1,b=-2.当a=1,b=-2时,3a-2b=3×1-2×(-2)=7;当a=-1,b=-2时,3a-2b=3×(-1)-2×(-2)=1.所以3a-2b的值是7或1.

11. 已知$a,b$互为相反数,$c,d$互为倒数,$m$的绝对值是2,则$\frac{|a+b|}{m^{2}+2}+4m-3cd$的值为5或-11.

答案： 5或-11 解析:因为a,b互为相反数,c,d互为倒数,m的绝对值是2,所以a+b=0,cd=1,m=2或m=-2.当m=2时,$\frac{|a+b|}{m²+2}$+4m-3cd=0+4×2-3×1=5;当m=-2时,$\frac{|a+b|}{m²+2}$+4m-3cd=0+4×(-2)-3×1=-11.所以$\frac{|a+b|}{m²+2}$+4m-3cd的值为5或-11.