第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图所示的圈分别表示负数、整数和正数,其中有甲、乙、丙三部分,关于这三部分的数,下列说法中正确的是(
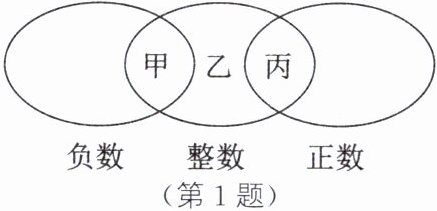
A.甲、丙两部分有无数个数,乙部分只有一个数且是0
B.甲、乙、丙三部分都有无数个数
C.甲、乙、丙三部分都只有一个数
D.甲部分只有一个数,乙、丙两部分有无数个数
A
)
A.甲、丙两部分有无数个数,乙部分只有一个数且是0
B.甲、乙、丙三部分都有无数个数
C.甲、乙、丙三部分都只有一个数
D.甲部分只有一个数,乙、丙两部分有无数个数
答案:
A 解析:由题意知,乙部分只有一个数且是0.因为正整数和负整数均有无数个,所以甲、丙两部分都有无数个数.
2. 下列各组数中,互为相反数的是(
A.|-2/3|与-(-2/3)
B.|-2/3|与-|-3/2|
C.|-2/3|与+(-2/3)
D.|-2/3|与|-3/2||
C
)A.|-2/3|与-(-2/3)
B.|-2/3|与-|-3/2|
C.|-2/3|与+(-2/3)
D.|-2/3|与|-3/2||
答案:
C 解析:$|-\frac{2}{3}|=\frac{2}{3}$,$-(-\frac{2}{3})=\frac{2}{3}$,两数相等,不互为相反数,故A不符合题意;$|-\frac{2}{3}|=\frac{2}{3}$,$-|-\frac{3}{2}|=-\frac{3}{2}$,两数不互为相反数,故B不符合题意;$|-\frac{2}{3}|=\frac{2}{3}$,$+(-\frac{2}{3})=-\frac{2}{3}$,两数互为相反数,故C符合题意;$|-\frac{2}{3}|=\frac{2}{3}$,$|-\frac{3}{2}|=\frac{3}{2}$,两数不互为相反数,故D不符合题意.
3. 给出下列判断:① 若|m|>0,则m>0;② 若m>n,则|m|>|n|;③若|m|>|n||,则m>n;④ 取任意有理数m,则|m|是正数;⑤ 在数轴上离原点越远,该点表示的数的绝对值越大.其中,正确的个数为(
A.0
B.1
C.2
D.3
B
)A.0
B.1
C.2
D.3
答案:
B 解析:若|m|>0,则m<0或m>0,故①错误.取m=1,n=-2,则1>-2,但|1|<|-2|,故②错误.取m=-2,n=1,则|-2|>|1|,但-2<1,故③错误.取任意有理数m,则|m|是正数或0,故④错误.根据绝对值的定义可知,在数轴上,离原点越远,该点表示的数的绝对值越大,故⑤正确.综上所述,正确的个数为1.
4. 在数轴上,点A,B表示的数互为相反数,且两点之间的距离是12个单位长度.点A沿着数轴先向右运动2秒.再向左运动5秒到达点C的位置.若点A的运动速度为每秒1.5个单位长度,则点C表示的数的相反数为
-1.5或10.5
.
答案:
-1.5或10.5 解析:因为点A,B表示的数互为相反数,且两点之间的距离是12个单位长度,所以点A表示的数为6或-6.因为点A向右移动了$2×1.5=3$(个)单位长度,向左移动了$5×1.5=7.5$(个)单位长度,所以点C在数轴上表示的数为$6+3-7.5=1.5$或$-6+3-7.5=-10.5$.所以点C表示的数的相反数为-1.5或10.5.
5. 如图,数轴上a的绝对值是b的绝对值的3倍,则数轴的原点在点
C
或点D
处(填“A” “B”“C”或“D”).
答案:
C D 解析:当原点在a,b之间时,因为a的绝对值是b的绝对值的3倍,所以原点在点C的位置.当原点在b的右侧时,因为a的绝对值是b的绝对值的3倍,所以原点在点D的位置.当原点在a的左侧时,因为a的绝对值是b的绝对值的3倍,所以这种情况不存在.综上所述,数轴的原点在点C或点D处.
6. 如图,直线上相邻两点的距离为1个单位长度,点A,B表示的数互为相反数.

(1)点C表示的数是什么?
(2)把直线补成一条数轴,并在数轴上表示:3 1/4,-3,-(-1.5),-|-1|.
(3)将(2)中各数按由小到大的顺序用“<”连接起来.

(1)点C表示的数是什么?
(2)把直线补成一条数轴,并在数轴上表示:3 1/4,-3,-(-1.5),-|-1|.
(3)将(2)中各数按由小到大的顺序用“<”连接起来.
答案:
(1)点C表示的数是-4.
(2)如图所示.
(3)$-3<-|-1|<-(-1.5)<3\frac{1}{4}$.
(2)如图所示.
(3)$-3<-|-1|<-(-1.5)<3\frac{1}{4}$.
7.一条直线流水线上依次右5个机器人,它们站位置在数轴上依次由点$A_1,A_2,A_3,A_4,A_5$表示(如图).

(1)站在哪点上的机器人表示数的绝对值最大?站在哪两个点上机器人表示的数到原点距离相等?
(2)怎样移动点$A_3,$使它先到达点$A_2,$再到达点$A_5? (3)$若原点是零件供应点,则5个机器人分别到达供应点取货路程是多少?

(1)站在哪点上的机器人表示数的绝对值最大?站在哪两个点上机器人表示的数到原点距离相等?
(2)怎样移动点$A_3,$使它先到达点$A_2,$再到达点$A_5? (3)$若原点是零件供应点,则5个机器人分别到达供应点取货路程是多少?
答案:
(1)因为|-4|最大,所以站在点$A_1$上的机器人表示的数的绝对值最大.因为|-3|=|3|,|-1|=|1|,所以站在点$A_2$和点$A_5$、点$A_3$和点$A_4$上的机器人表示的数到原点的距离相等.
(2)将点$A_3$先向左移动2个单位长度到达点$A_2$,再向右移动6个单位长度到达点$A_5$.
(3)$|-4|+|-3|+|-1|+|1|+|3|=12$,所以5个机器人分别到达供应点取货的总路程是12.
(2)将点$A_3$先向左移动2个单位长度到达点$A_2$,再向右移动6个单位长度到达点$A_5$.
(3)$|-4|+|-3|+|-1|+|1|+|3|=12$,所以5个机器人分别到达供应点取货的总路程是12.
查看更多完整答案,请扫码查看


