《2025年优化探究同步导学案高中数学必修第一册人教版》

二次函数的解析式有三种:
一般式$:y$$f(x)=ax^2+bx+c(a\neq0)$$= ax^2 + bx + c(a\neq0);$
顶点式$:y$$f(x)=a(x - h)^2+k(a\neq0)$$= a(x - h)^2 + k(a\neq0);$
交点式$:y$$f(x)=a(x - x_1)(x - x_2)(a\neq0)$$= a(x - x_1)(x - x_2)(a\neq0).$

答案： $f(x)=ax^2+bx+c(a\neq0)$ $f(x)=a(x - h)^2+k(a\neq0)$ $f(x)=a(x - x_1)(x - x_2)$ $(a\neq0)$

[例2] 某企业生产一种机器的固定成本为0.5万元,但每生产1百台机器时,又需可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为5百台,销售收入(单位:万元)的函数为$F(x)=5x-\frac{1}{2}x^2(0\leqslant x\leqslant5)$,其中$x$是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)当年产量是多少时,企业所得利润最大?
[分析] (1)根据“利润=销售收入-成本”可求解.(2)由利润函数是二次函数,知可以利用二次函数的性质求出函数取最大值时对应的自变量$x$的值.

答案： [解]
(1)设利润函数为$G(x)$，成本函数为$R(x)$，则依题意得，当$0\leq x\leq5$时，产品能够全部售出，当$x＞5$时，只能销售$5$百台，所以$G(x)=F(x)-R(x)=$ $\begin{cases}(5x-\frac{1}{2}x^2)-(0.5 + 0.25x),0\leq x\leq5,\\5×5-\frac{1}{2}×5^2-(0.5 + 0.25x),x＞5,\end{cases}$整理，得$G(x)=$ $\begin{cases}-0.5x^2+4.75x - 0.5,0\leq x\leq5,\\12 - 0.25x,x＞5.\end{cases}$
(2)由
(1)知当$0\leq x\leq5$时，利润函数$G(x)$ $=-0.5x^2+4.75x - 0.5$，当$x=4.75$时，$G(x)$有最大值，$G(x)_{ max}\approx$ $10.78$(万元)；当$x＞5$时，$G(x)_{ max}＜12 - 0.25×5=$ $10.75$(万元)。所以当年产量为$475$台时，企业所得利润最大.

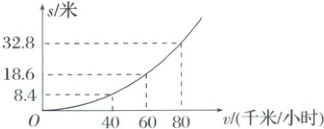
2. 近年来,我国新能源汽车制造业蓬勃发展,某著名汽车企业自主创新,研发了一款新能源汽车,经过大数据分析获得,在某种路面上,该品牌汽车的刹车距离$s$(米)与其车速$v$(千米/小时)满足下列关系:$s=\frac{v^2}{200}+mv + n$($m,n$是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据该新能源汽车的实验数据绘制的刹车距离$s$(米)与该车的车速$v$(千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为$y_1 = 4.1x - 0.1x^2$,在乙地的销售利润(单位:万元)为$y_2 = 2x$,其中$x$为销售量(单位:辆).

(1)若该公司在两地共销售20辆该品牌的新能源汽车,则能获得的最大利润$L$是多少?
(2)如果要求刹车距离不超过25.2米,求该品牌新能源汽车行驶的最大速度.

答案： 跟踪训练2.解：
(1)设该公司在甲地销售该品牌的新能源汽车$x$辆，则在乙地销售该品牌的汽车$(20 - x)$辆，$x\in[0,20]$，且$x\in N^*$。依题意，可得利润$L=4.1x - 0.1x^2+ 2(20 - x)= - 0.1x^2+2.1x + 40$。因为$x\in [0,20]$，且$x\in N^*$，所以，当$x = 10$或$x=$ $11$时，$L_{ max}=51$。即当甲地销售该品牌的新能源汽车$10$辆或$11$辆时，公司获得的总利润最大值为$51$万元. $\begin{cases}\frac{40^2}{200}+40m + n=8.4,\frac{60^2}{200}+60m + n=18.6,\end{cases}$解得$m=\frac{1}{100},n=0$，所以$s=\frac{v^2}{200}+\frac{v}{100}(v\geq 0)$。令$\frac{v^2}{200}+\frac{v}{100}\leq25.2$，即$v^2+2v - 5040\leq0$，解得$-72\leq v\leq70$。因为$v\geq0$，所以$0\leq v$ $\leq70$。故该新能源汽车行驶的最大速度是$70$千米/小时.