《2025年评优监测课时作业八年级数学上册苏科版》

7. 拖拉机耕地，油箱内装有油$ 42 $升，如果每小时耗油$ 5 $升，写出所剩油量$ w $（升）与时间$ t $（小时）之间的函数表达式$w = 42 - 5t$，其中42,5是常量，w,t是变量。

答案： 函数表达式：$w = 42 - 5t$；
常量是：$42$和$5$（或写成$42,5$ ）；
变量是：$w$和$t$（或 $t,w$）。

8. 从高楼楼顶掉下一个物体，物体下落的距离$ s( m) $与下落的时间$ t( s) $有$ s = \frac{1}{2} × 9.8t^{2} $的关系，根据表达式填写下表：

从上表可知$t$是自变量，$s$是$t$的函数。

答案： |下落的时间$ t/ s $|1|2|3|4|…|
|----|----|----|----|----|----|
|下落的距离$ s/ m $|4.9|19.6|44.1|78.4|…|
从上表可知$t$是自变量，$s$是$t$的函数。
故答案为$t$；$s$；$t$

9. 某剧院的观众席的座位为扇形，且按下列方式设置：

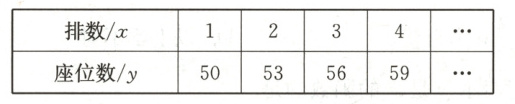
（1）按照上表所示的规律，当排数为$ 6 $时，此时座位数为65；
（2）写出座位数$ y $与排数$ x $之间的关系式：$y = 3x + 47$；
（3）按照上表所示的规律，某一排可能有$ 90 $个座位吗？说说你的理由。

答案： （1）65
（2）$y = 3x + 47$
（3）不可能。理由：令$3x + 47 = 90$，解得$x = \frac{43}{3}$，不是正整数，故某一排不可能有90个座位。

10. 物理实验证实：在弹性范围内，某弹簧长度$ y( cm) $与所挂物体质量$ x( kg) $满足函数关系$ y = kx + 15 $。下表是测量物体质量时，该弹簧长度与所挂物体质量的数量关系。
（1）求$ y $与$ x $的函数表达式；
（2）当弹簧长度为$ 20 cm $时，求所挂物体的质量。

答案：
(1)
根据表格数据，当$x = 0$时，$y = 15$；当$x = 2$时，$y = 19$。
代入$y = kx + 15$，得$19 = 2k + 15$，
解得$k = 2$。
所以$y$与$x$的函数表达式为$y = 2x + 15$。
(2)
当$y = 20$时，代入$y = 2x + 15$，
得$20 = 2x + 15$，
解得$x = 2.5$。
所以当弹簧长度为$20cm$时，所挂物体的质量为$2.5kg$。