第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
7. 某学习小组在数学活动课上设计了一个问题情境:已知林茂的家、体育场、文具店在同一条直线上,林茂从家匀速跑步 15 min 到体育场,在体育场锻炼了一阵后又匀速走到文具店买笔,然后匀速走回家.给出的图象反映了这个过程中林茂离家的距离$y km$与离开家的时间$x min$之间的对应关系.请根据相关信息,解决下列问题:
(1)填空:
①体育场到文具店的距离为
②林茂从文具店到家的行进速度为
③当林茂离家的距离为$2 km$时,他离开家的时间为
(2)当$15\leq x\leq45$时,请求出$y$关于$x$的函数表达式.

(1)填空:
①体育场到文具店的距离为
1
$km$;②林茂从文具店到家的行进速度为
0.06
$km/min$;③当林茂离家的距离为$2 km$时,他离开家的时间为
12或37.5
$min$;(2)当$15\leq x\leq45$时,请求出$y$关于$x$的函数表达式.

答案:
(1)①1
②0.06
③12或37.5
(2)当15≤x≤30时,y=2.5;当30<x≤45时,设y=kx+b,将(30,2.5),(45,1.5)代入得:
$\begin{cases}2.5=30k+b\\1.5=45k+b\end{cases}$
解得$\begin{cases}k=-\frac{1}{15}\\b=\frac{9}{2}\end{cases}$,故y=$-\frac{1}{15}x+\frac{9}{2}$
综上,当15≤x≤45时,$y=\begin{cases}2.5&(15\leq x\leq30)\\-\frac{1}{15}x+\frac{9}{2}&(30<x\leq45)\end{cases}$
(1)①1
②0.06
③12或37.5
(2)当15≤x≤30时,y=2.5;当30<x≤45时,设y=kx+b,将(30,2.5),(45,1.5)代入得:
$\begin{cases}2.5=30k+b\\1.5=45k+b\end{cases}$
解得$\begin{cases}k=-\frac{1}{15}\\b=\frac{9}{2}\end{cases}$,故y=$-\frac{1}{15}x+\frac{9}{2}$
综上,当15≤x≤45时,$y=\begin{cases}2.5&(15\leq x\leq30)\\-\frac{1}{15}x+\frac{9}{2}&(30<x\leq45)\end{cases}$
8. 一艘游轮从无锡出发前往苏州,线路如图 1 所示.当游轮到达“三山景点”时,一艘货轮沿着同样的线路从无锡出发前往苏州.已知游轮的速度为$20 km/h$,游轮行驶的时间记为$x(h)$,两艘轮船距离无锡的路程$y(km)$关于$x(h)$的函数图象如图 2 所示(游轮在停靠前后的行驶速度不变).当游轮从“三山景点”再次出发时,游轮与货轮之间的距离缩短了$50 km$.
(1)写出图 2 中 C 点的实际意义是
(2)求图 2 中 BC 对应的函数表达式及自变量$x$的取值范围;
(3)求游轮、货轮相遇时$x$的值.
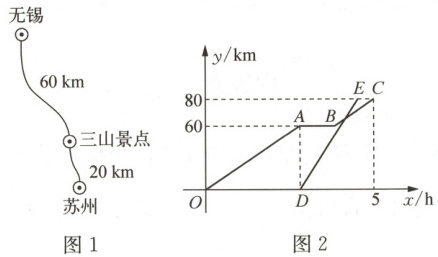
图 1 图 2
(1)写出图 2 中 C 点的实际意义是
游轮行驶5小时后到达苏州,距离无锡80km。
;(2)求图 2 中 BC 对应的函数表达式及自变量$x$的取值范围;
(3)求游轮、货轮相遇时$x$的值.

图 1 图 2
答案:
(1)游轮行驶5小时后到达苏州,距离无锡80km。
(2)设BC对应的函数表达式为y=kx+b,B(4,60),C(5,80)。代入得:60=4k+b,80=5k+b,解得k=20,b=-20。表达式为y=20x-20,自变量取值范围4≤x≤5。
(3)货轮速度:从x=3到x=4,1小时行驶50km,速度50km/h,表达式y=50(x-3)=50x-150。游轮BC段y=20x-20。令20x-20=50x-150,解得x=13/3。
相遇时x的值为13/3。
(1)游轮行驶5小时后到达苏州,距离无锡80km。
(2)设BC对应的函数表达式为y=kx+b,B(4,60),C(5,80)。代入得:60=4k+b,80=5k+b,解得k=20,b=-20。表达式为y=20x-20,自变量取值范围4≤x≤5。
(3)货轮速度:从x=3到x=4,1小时行驶50km,速度50km/h,表达式y=50(x-3)=50x-150。游轮BC段y=20x-20。令20x-20=50x-150,解得x=13/3。
相遇时x的值为13/3。
查看更多完整答案,请扫码查看


