第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
10. 某校八年级(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度$CE$,他们进行了如下操作:
① 测得水平距离$BD$的长为$12$米;
② 根据手中剩余线的长度计算出风筝线$BC$的长为$20$米;
③ 牵线放风筝的小明的身高为$1.6$米.
(1) 求风筝的垂直高度$CE$;
(2) 如果小明想风筝沿$CD$方向下降$11$米到点$M$,则他应该往回收线多少米?
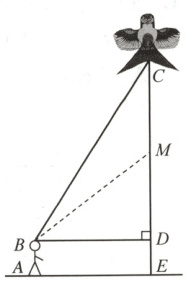
① 测得水平距离$BD$的长为$12$米;
② 根据手中剩余线的长度计算出风筝线$BC$的长为$20$米;
③ 牵线放风筝的小明的身高为$1.6$米.
(1) 求风筝的垂直高度$CE$;
(2) 如果小明想风筝沿$CD$方向下降$11$米到点$M$,则他应该往回收线多少米?

答案:
(1) 在Rt△BCD中,∠BDC=90°,BC=20米,BD=12米。
由勾股定理得:$CD^2 + BD^2 = BC^2$,
则$CD = \sqrt{BC^2 - BD^2} = \sqrt{20^2 - 12^2} = \sqrt{400 - 144} = \sqrt{256} = 16$米。
∵小明身高为1.6米,即$DE = 1.6$米,
∴风筝的垂直高度$CE = CD + DE = 16 + 1.6 = 17.6$米。
(2) 风筝沿CD方向下降11米到点M,得$CM = 11$米,
则$MD = CD - CM = 16 - 11 = 5$米。
在Rt△BMD中,∠BDM=90°,BD=12米,MD=5米,
由勾股定理得:$BM = \sqrt{BD^2 + MD^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13$米。
∴回收线长度为$BC - BM = 20 - 13 = 7$米。
(1) 17.6米;
(2) 7米。
(1) 在Rt△BCD中,∠BDC=90°,BC=20米,BD=12米。
由勾股定理得:$CD^2 + BD^2 = BC^2$,
则$CD = \sqrt{BC^2 - BD^2} = \sqrt{20^2 - 12^2} = \sqrt{400 - 144} = \sqrt{256} = 16$米。
∵小明身高为1.6米,即$DE = 1.6$米,
∴风筝的垂直高度$CE = CD + DE = 16 + 1.6 = 17.6$米。
(2) 风筝沿CD方向下降11米到点M,得$CM = 11$米,
则$MD = CD - CM = 16 - 11 = 5$米。
在Rt△BMD中,∠BDM=90°,BD=12米,MD=5米,
由勾股定理得:$BM = \sqrt{BD^2 + MD^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13$米。
∴回收线长度为$BC - BM = 20 - 13 = 7$米。
(1) 17.6米;
(2) 7米。
11. 如图,圆柱形玻璃杯的高为$16 cm$,底面周长为$24 cm$.一只蚂蚁在杯外壁、离杯上沿$5.5 cm$的点$A$处.蚂蚁发现,在与它相对的杯壁点$B$处有一滴蜂蜜,已知点$B$距离杯底$5.5 cm$.
(1) 若蜂蜜在杯外壁,蚂蚁至少爬行多远就能吃到蜂蜜?
(2) 若蜂蜜在杯内壁,蚂蚁要吃到蜂蜜,最少应爬行多远(杯壁厚度不计)?

(1) 若蜂蜜在杯外壁,蚂蚁至少爬行多远就能吃到蜂蜜?
(2) 若蜂蜜在杯内壁,蚂蚁要吃到蜂蜜,最少应爬行多远(杯壁厚度不计)?

答案:
(1) 将圆柱侧面展开为长方形,长=底面周长=24cm,宽=圆柱高=16cm。点A在杯外壁离上沿5.5cm,距杯底16-5.5=10.5cm;点B在相对外壁距杯底5.5cm。两点水平距离为底面周长一半=12cm,垂直距离=10.5-5.5=5cm。由勾股定理,最短距离=√(12²+5²)=13cm。
(2) 蜂蜜在杯内壁,将内壁点B对称至外壁得B',此时A与B'垂直距离=10.5+5.5=16cm(圆柱高),水平距离=12cm。由勾股定理,最短距离=√(12²+16²)=20cm。
(1)13cm;
(2)20cm。
(1) 将圆柱侧面展开为长方形,长=底面周长=24cm,宽=圆柱高=16cm。点A在杯外壁离上沿5.5cm,距杯底16-5.5=10.5cm;点B在相对外壁距杯底5.5cm。两点水平距离为底面周长一半=12cm,垂直距离=10.5-5.5=5cm。由勾股定理,最短距离=√(12²+5²)=13cm。
(2) 蜂蜜在杯内壁,将内壁点B对称至外壁得B',此时A与B'垂直距离=10.5+5.5=16cm(圆柱高),水平距离=12cm。由勾股定理,最短距离=√(12²+16²)=20cm。
(1)13cm;
(2)20cm。
查看更多完整答案,请扫码查看


