《2025年同步解析与测评学考练九年级数学上册人教版》

5. (2024·吉林长春中考)若抛物线$y = x^{2}-x + c(c$是常数)与$x$轴没有交点,则$c$的取值范围是$c＞\dfrac{1}{4}$。

答案： $c＞\dfrac{1}{4}$

6. (2024·四川成都中考)在平面直角坐标系$xOy$中,$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,$C(x_{3},y_{3})是二次函数y = -x^{2}+4x - 1$图象上的三点。若$0 ＜ x_{1} ＜ 1$,$x_{2} ＞ 4$,则$y_{1}$＞$y_{2}$(填“$＞$”或“$＜$”)；若对于$m ＜ x_{1} ＜ m + 1$,$m + 1 ＜ x_{2} ＜ m + 2$,$m + 2 ＜ x_{3} ＜ m + 3$,存在$y_{1} ＜ y_{3} ＜ y_{2}$,则$m$的取值范围是$-\dfrac{1}{2}＜m＜1$。

答案： $＞ -\dfrac{1}{2}＜m＜1$

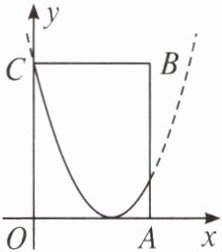
7. (2023·浙江绍兴中考)在平面直角坐标系$xOy$中,一个图形上的点都在一边平行于$x$轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形。例如：如图,函数$y = (x - 2)^{2}(0\leq x\leq3)$的图象(抛物线中的实线部分),它的关联矩形为矩形$OABC$。若二次函数$y = \frac{1}{4}x^{2}+bx + c(0\leq x\leq3)图象的关联矩形恰好也是矩形OABC$,则$b=$$\dfrac{7}{12}$或$-\dfrac{25}{12}$。

答案： $\dfrac{7}{12}$或$-\dfrac{25}{12}$

8. (2021·四川遂宁中考改编)某服装店以每件$30$元的价格购进一批上衣,如果以每件$40$元出售,那么一个月内能售出$300$件。根据以往销售经验,销售单价每提高$1$元,销售量就会减少$10$件,设上衣的销售单价提高$x$元。
(1)服装店希望一个月内销售该种上衣能获得利润$3360$元,并且尽可能减少库存,问上衣的销售单价应提高多少元？
(2)当销售单价定为多少元时,该服装店一个月内销售这种上衣获得的利润最大？最大利润是多少元？

答案： 解
(1)设上衣的销售单价提高x元.
由题意列方程,得(x+40-30)(300-10x)=3360,
解得$x_{1}=2,x_{2}=18,$
∵要尽可能减少库存,
∴$x_{2}=18$不合题意,应舍去.
∴上衣的销售单价应提高2元.
(2)设利润为M元,由题意可得
$M=(x+40-30)(300-10x)=-10x^{2}+200x+3000=-10(x-10)^{2}+4000,$
∴当x=10时$,M_{最大值}=4000$元,
∴销售单价为40+10=50(元).
∴当服装店将销售单价定为50元时,得到最大利润是4000元.