《2025年同步解析与测评学考练九年级数学上册人教版》

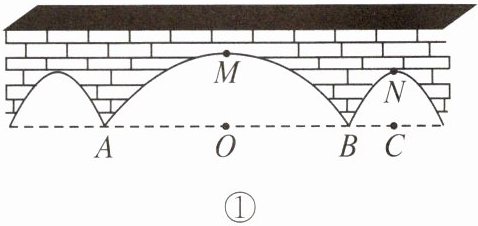
3. 如图①,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同。正常水位时,大孔水面宽度$AB = 20m$,顶点$M距水面6m(MO = 6m)$,小孔顶点$N距水面4.5m(NC = 4.5m)$。当水位上涨刚好淹没小孔时,借助图②中的直角坐标系,求此时大孔的水面宽度$EF$。

答案： 解 设大孔对应的抛物线的函数解析式为$y=ax^{2}+6,$
依题意,得点B的坐标为(10,0),
所以$a×10^{2}+6=0,$
解得a=-0.06,
即$y=-0.06x^{2}+6.$
当y=4.5时$,-0.06x^{2}+6=4.5,$
解得x=±5.
因此EF=10m,
即大孔的水面宽度为10m.

1. (2022·浙江衢州中考)已知二次函数$y = a(x - 1)^{2}-a(a\neq0)$,当$-1\leq x\leq4$时,$y的最小值为-4$,则$a$的值为(D)
A.$\frac{1}{2}或4$
B.$\frac{4}{3}或-\frac{1}{2}$
C.$-\frac{4}{3}或4$
D.$-\frac{1}{2}或4$

答案： D 函数$y=a(x-1)^{2}-a$图象的对称轴为直线x=1,顶点坐标为(1,-a).
当a＞0时,在-1≤x≤4,y有最小值-a.
∵y的最小值为-4,
∴-a=-4,
∴a=4;
当a＜0时,在-1≤x≤4,y有最小值8a,
∴$8a=-4,a=-\dfrac{1}{2}.$
综上所述,a的值为4或$-\dfrac{1}{2}.$故选D.

2. (2022·内蒙古通辽中考)在平面直角坐标系中,将二次函数$y = (x - 1)^{2}+1$的图象向左平移1个单位长度,再向下平移$2$个单位长度,所得图象对应的函数的解析式为(D)
A.$y = (x - 2)^{2}-1$
B.$y = (x - 2)^{2}+3$
C.$y = x^{2}+1$
D.$y = x^{2}-1$

答案： D 将二次函数$y=(x-1)^{2}+1$的图象向左平移1个单位长度,再向下平移2个单位长度,得到的图象对应的函数解析式是$y=(x-1+1)^{2}+1-2,$即$y=x^{2}-1.$故选D.

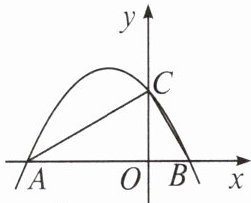
3. (2022·贵州铜仁中考)如图,若抛物线$y = ax^{2}+bx + c(a\neq0)与x轴交于A$,$B$两点,与$y轴交于点C$。若$\angle OAC = \angle OCB$,则$ac$的值为(A)

A.$-1$
B.$-2$
C.$-\frac{1}{2}$
D.$-\frac{1}{3}$

答案： A 设点$A(x_{1},0),B(x_{2},0),C(0,c),$
∵二次函数$y=ax^{2}+bx+c$的图象过点C(0,c),
∴OC=c.
∵∠OAC=∠OCB,OC⊥AB,
∴△OAC∽△OCB,
∴$\dfrac{OA}{OC}=\dfrac{OC}{OB},$
∴$OC^{2}=OA·OB,$
即|$x_{1}·x_{2}$|$=c^{2}=-x_{1}·x_{2}.$
令$ax^{2}+bx+c=0,$根据根与系数的关系知$x_{1}·x_{2}=\dfrac{c}{a},$
∴$-x_{1}x_{2}=-\dfrac{c}{a}=c^{2},$故ac=-1,故选A.

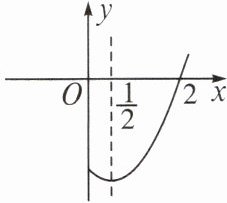
4. (2021·四川达州中考)如图,已知抛物线$y = ax^{2}+bx + c(a,b,c$为常数,$a\neq0)$经过点(2,0),且对称轴为直线$x = \frac{1}{2}$,有下列结论：①$abc ＞ 0$；②$a + b ＞ 0$；③$4a + 2b + 3c ＜ 0$；④无论$a,b,c$取何值,抛物线一定经过$(\frac{c}{2a},0)$；⑤$4am^{2}+4bm - b\geq0$。其中正确结论有(D)

A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： D