《2025年同步解析与测评学考练九年级数学上册人教版》

4. 某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为$4$万元,可变成本逐年增长. 已知该养殖户第$1年的可变成本为2.6$万元. 设可变成本平均每年增长的百分率为$x$. 用含$x的代数式表示第3$年的可变成本为$2.6(1+x)^{2}$万元.

答案： $2.6(1+x)^{2}$

【例1】某市从$2022$年起连续投入资金用于改造老旧小区. 已知每年投入资金的增长率相同,其中$2022年投入资金10000$万元,$2024年投入资金14400$万元.
(1)求该市改造老旧小区投入资金的年平均增长率；
(2)$2024年老旧小区改造的平均费用为每个800$万元,$2025$年该市为提高老旧小区品质,每个小区改造费用计划增加$20\%$. 如果投入资金年增长率保持不变,求该市$2025$年最多可以改造多少个老旧小区？

答案： 分析
(1)$2022年投入资金×(1 +年平均增长率)^2 = 2024$年投入资金,列出方程求出年平均增长率；
(2)设该市在$2025年可以改造y$个老旧小区,根据题意列出不等式,解之取其中的最大整数值即可得出结论.
解
(1)设该市改造老旧小区投入资金的年平均增长率为$x$,
依题意得$10000(1 + x)^2 = 14400$,
解得$x_1 = 0.2 = 20\%$,$x_2 = -2.2$(不合题意,舍去).
答：该市改造老旧小区投入资金的年平均增长率为$20\%$.
(2)设该市在$2025年可以改造y$个老旧小区,
依题意得$800×(1 + 20\%)y \leq 14400×(1 + 20\%)$,解得$y \leq 18$,
又$y$为整数,故$y的最大值为18$.
答：该市在$2025年最多可以改造18$个老旧小区.

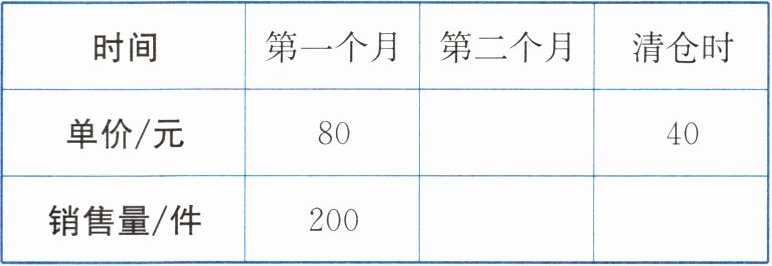
【例2】某批发商以每件$50元的价格购进800件T$恤. 第一个月以单价$80$元销售,售出了$200$件；第二个月如果单价不变,预计仍可售出$200$件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低$1$元,可多售出$10$件,但最低单价应高于购进的价格；第二个月结束后,批发商将对剩余的$T$恤一次性清仓销售,清仓时单价为$40$元. 设第二个月单价降低$x$元.
(1)填表(不需要化简).

(2)如果批发商希望通过销售这批$T恤获利9000$元,那么第二个月的单价应为多少元？

答案： 分析
(1)由“第二个月单价降低$x$元”知第二个月的单价为$(80 - x)$元,销售量为$(200 + 10x)$件,清仓时的销售量为总数量减去前面两个月的销售量,即$800 - 200 - (200 + 10x)$；
(2)销售额$-成本= $利润,由“获利$9000$元”建立方程,得$80×200 + (80 - x)(200 + 10x) + 40[800 - 200 - (200 + 10x)] - 50×800 = 9000$,化简后求解即可.
解
(1)$80 - x$,$200 + 10x$,$800 - 200 - (200 + 10x)$；
(2)根据题意,得$80×200 + (80 - x)\cdot(200 + 10x) + 40[800 - 200 - (200 + 10x)] - 50×800 = 9000$.
整理,得$x^2 - 20x + 100 = 0$,
解方程得$x_1 = x_2 = 10$.
当$x = 10$时,$80 - x = 70 ＞ 50$.
答：第二个月的单价应为$70$元.