《2025年同步解析与测评学考练九年级数学上册人教版》

9. 已知圆锥的底面半径为$4\mathrm{cm}$,高为$5\mathrm{cm}$,则它的表面积为(D)
A.$12\pi\mathrm{cm}^2$
B.$26\pi\mathrm{cm}^2$
C.$\sqrt{41}\pi\mathrm{cm}^2$
D.$(4\sqrt{41}+16)\pi\mathrm{cm}^2$

答案： D

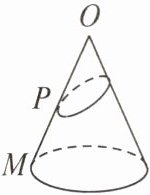
10. 已知点O为一圆锥的顶点,点M为该圆锥底面上一点,点P在母线OM上,一只蚂蚁从点P出发,绕圆锥侧面爬行,回到点P时所爬过的最短路线的痕迹如图所示. 若沿母线OM将圆锥侧面剪开并展开,则所得侧面展开图是(D)

答案： D

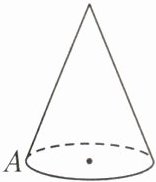
11. 如图,圆锥的底面半径为$5$,母线长为$20$,一只蜘蛛从底面圆周上一点$A出发沿圆锥的侧面爬行一周后回到点A$的最短路程是20$\sqrt{2}$.

答案： 20$\sqrt{2}$

12. 如图,这是一个由圆柱形材料加工而成的零件,它是以圆柱的上底面为底面,在其内部“掏取”一个与圆柱等高的圆锥而得到的,其底面直径$AB= 12\mathrm{cm}$,高$BC= 8\mathrm{cm}$,求这个零件的全面积.(结果保留根号)

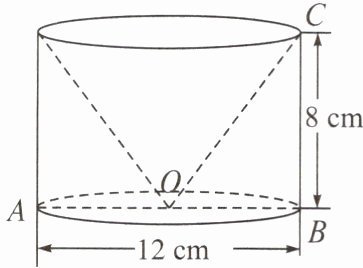
答案： 解：这个零件的底面积为
π×($\frac{12}{2}$)² = 36π(cm²)，
这个零件的外侧面积为
12π×8 = 96π(cm²)，
圆锥母线长
OC = $\sqrt{8^{2}+(\frac{12}{2})^{2}}$ = 10(cm)，
这个零件的内侧面积为
$\frac{1}{2}$×12π×10 = 60π(cm²)，
所以这个零件的全面积为
36π + 96π + 60π = 192π(cm²).

★13. 如图①,在正方形的铁皮上剪下一个圆形和一个扇形,使之恰好围成如图②的一个圆锥,设图①中圆的半径为$r$,扇形的半径为$R$,那么扇形的半径$R与\odot O的半径r$之间满足怎样的关系？并说明理由.

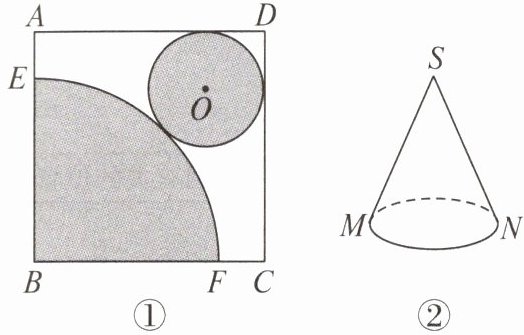
答案： 解：扇形的半径R等于⊙O的半径r的4倍，
理由如下:
因为$\overset{\frown}{EF}$ = 2πR×$\frac{1}{4}$ = $\frac{1}{2}$πR，⊙O的周长为2πr，
且题图①中的扇形和⊙O能围成题图②的圆锥，
所以$\frac{1}{2}$πR = 2πr，
即R = 4r.

★14. 如图,一个纸杯的母线延长后相交于一点,形成的立体图形是圆锥,该圆锥的侧面展开图是扇形$OAB$,经测量,纸杯上开口圆的直径是$6\mathrm{cm}$,下底圆直径为$4\mathrm{cm}$,母线长$EF= 8\mathrm{cm}$. 求扇形$OAB$的圆心角及这个纸杯的全面积.(面积计算结果用$\pi$表示)

答案： 解：由题意，知$\overset{\frown}{AB}$ = 6π cm，$\overset{\frown}{CD}$ = 4π cm.
设∠AOB = n°，AO = R cm，
则CO = (R - 8)cm，
根据弧长公式，
得$\frac{n\pi R}{180}$ = 6π，$\frac{n\pi(R - 8)}{180}$ = 4π.
解得n = 45，R = 24.
所以扇形圆心角的度数为45°.
由R = 24，得R - 8 = 16.
所以S扇形OCD = $\frac{1}{2}$×4π×16 = 32π(cm²)，
S扇形OAB = $\frac{1}{2}$×6π×24 = 72π(cm²).
所以S纸杯侧 = S扇形OAB - S扇形OCD = 72π - 32π = 40π(cm²).
又因为S纸杯底 = π($\frac{4}{2}$)² = 4π(cm²)，
所以S纸杯全 = 40π + 4π = 44π(cm²).