第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 如图,用长为 $ 12m $ 的木方做一个有一条横档的矩形窗户,为使透进的光线最多,选择窗户的高 $ AB $(木方粗细忽略不计)为(
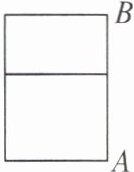
A.$ 1m $
B.$ 2m $
C.$ 3m $
D.$ 4m $
C
)
A.$ 1m $
B.$ 2m $
C.$ 3m $
D.$ 4m $
答案:
C
2. 某商场购进一批 $ L $ 型服装(数量足够多),进价为 $ 40 $ 元/件,以 $ 60 $ 元/件销售,每天销售 $ 20 $ 件。根据市场调研,若每件每降价 $ 1 $ 元,则每天销售数量比原来多 $ 3 $ 件。现商场决定对 $ L $ 型服装开展降价促销活动,每件降价 $ x $ 元($ x $ 为正整数)。在促销期间,商场要想每天获得最大销售毛利润,每件应降价
7
元,每天最大销售毛利润为533
元。(注:毛利润 $ = $ 销售价 $ - $ 进货价)
答案:
7 533
3. 如图,在边长为 $ 6cm $ 的正方形 $ ABCD $ 中,点 $ E $,$ F $,$ G $,$ H $ 分别从点 $ A $,$ B $,$ C $,$ D $ 同时出发,均以 $ 1cm/s $ 的速度向点 $ B $,$ C $,$ D $,$ A $ 匀速运动,当点 $ E $ 到达点 $ B $ 时,四个点同时停止运动,在运动过程中,当运动时间为
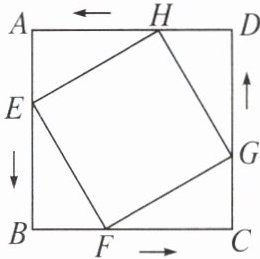
3
$ s $ 时,四边形 $ EFGH $ 的面积最小,其最小值是18
$ cm^{2} $。
答案:
3 18
4. 某农场拟建一间矩形小牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为 $ 50m $。设饲养室长为 $ x $(单位:$ m $),占地面积为 $ y $(单位:$ m^{2} $)。
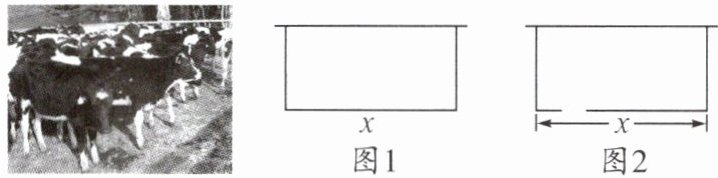
(1)如图 1,问饲养室长 $ x $ 为多少时,占地面积 $ y $ 最大?
(2)如图 2,现要求在图中所示位置留 $ 2m $ 宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多 $ 2m $ 就行了。”请你通过计算,判断小敏的说法是否正确。

(1)如图 1,问饲养室长 $ x $ 为多少时,占地面积 $ y $ 最大?
(2)如图 2,现要求在图中所示位置留 $ 2m $ 宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多 $ 2m $ 就行了。”请你通过计算,判断小敏的说法是否正确。
答案:
解
(1)$y = x\cdot\frac{50 - x}{2}=-\frac{1}{2}(x - 25)^{2}+\frac{625}{2}$,当$x = 25$时,y最大,即饲养室长x为25m时,占地面积y最大。
(2)由题意得$y = x\cdot\frac{50 - (x - 2)}{2}=-\frac{1}{2}(x - 26)^{2}+338$,当$x = 26$时,占地面积y最大,即饲养室长x为26m时,占地面积y最大;因为$26 - 25 = 1≠2$,所以小敏的说法不正确。
(1)$y = x\cdot\frac{50 - x}{2}=-\frac{1}{2}(x - 25)^{2}+\frac{625}{2}$,当$x = 25$时,y最大,即饲养室长x为25m时,占地面积y最大。
(2)由题意得$y = x\cdot\frac{50 - (x - 2)}{2}=-\frac{1}{2}(x - 26)^{2}+338$,当$x = 26$时,占地面积y最大,即饲养室长x为26m时,占地面积y最大;因为$26 - 25 = 1≠2$,所以小敏的说法不正确。
查看更多完整答案,请扫码查看


