第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
8. 如图,在$\triangle ABC$中,$AB = 3$,$AC = \frac{9}{4}$,点$D是BC$边上的一点,$AD = BD = 2DC$,设$\triangle ABD与\triangle ACD的内切圆半径分别为r_1$,$r_2$,则$\frac{r_1}{r_2} = $(
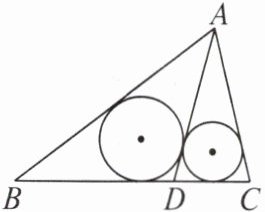
A.$2$
B.$\frac{4}{3}$
C.$\frac{3}{2}$
D.$\frac{2}{3}$
C
)
A.$2$
B.$\frac{4}{3}$
C.$\frac{3}{2}$
D.$\frac{2}{3}$
答案:
C
9. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3$,$AB = 5$,$D为BC$边的中点,以$AD上一点O为圆心的\odot O和AB$,$BC$均相切,则$\odot O$的半径为
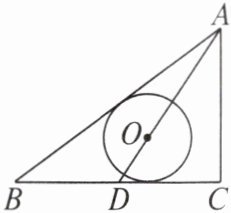
$\frac{6}{7}$
.
答案:
$\frac{6}{7}$
10. 如图,$AB为\odot O$的直径,$PQ与\odot O相切于点T$,$AC\perp PQ$,且垂足为$C$,交$\odot O于点D$.
(1)求证:$AT平分\angle BAC$;
(2)若$AD = 2$,$TC = \sqrt{3}$,求$\odot O$的半径.

(1)求证:$AT平分\angle BAC$;
(2)若$AD = 2$,$TC = \sqrt{3}$,求$\odot O$的半径.

答案:
(1)证明 如图,连接OT.

∵PQ与⊙O相切于点T,
∴OT⊥PQ.
又AC⊥PQ,
∴OT//AC,∠TAC=∠ATO.
又OT=OA,
∴∠ATO=∠OAT,∠OAT=∠TAC,
即AT平分∠BAC.
(2)解 过点O作OM⊥AC,垂足为M,
∴AM=MD=$\frac{AD}{2}$=1.
又∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,OM=TC=$\sqrt{3}$.
在Rt△AOM中,
AO=$\sqrt{O{M}^{2}+A{M}^{2}}$=$\sqrt{3 + 1}$=2,
即⊙O的半径为2.
(1)证明 如图,连接OT.

∵PQ与⊙O相切于点T,
∴OT⊥PQ.
又AC⊥PQ,
∴OT//AC,∠TAC=∠ATO.
又OT=OA,
∴∠ATO=∠OAT,∠OAT=∠TAC,
即AT平分∠BAC.
(2)解 过点O作OM⊥AC,垂足为M,
∴AM=MD=$\frac{AD}{2}$=1.
又∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,OM=TC=$\sqrt{3}$.
在Rt△AOM中,
AO=$\sqrt{O{M}^{2}+A{M}^{2}}$=$\sqrt{3 + 1}$=2,
即⊙O的半径为2.
★11. 阅读下列材料并回答问题.
材料:如果一个三角形的三边长分别为$a$,$b$,$c$,记$p = \frac{a + b + c}{2}$,那么三角形的面积为$S = \sqrt{p(p - a)(p - b)(p - c)}$. ①
古希腊几何学家海伦(Heron,约公元$50$年),在数学史上以解决几何测量问题而闻名. 他在《度量》一书中,给出了公式①和它的证明,这一公式称为海伦公式. 我国南宋数学家秦九韶(约$1202$ — 约$1261$),曾提出利用三角形的三边求面积的秦九韶公式$S = \sqrt{\frac{1}{4}\left[a^2b^2 - \left(\frac{a^2 + b^2 - c^2}{2}\right)^2\right]}$. ②
下面我们对公式②进行变形:
$\begin{aligned}&\sqrt{\frac{1}{4}\left[a^2b^2 - \left(\frac{a^2 + b^2 - c^2}{2}\right)^2\right]}\\=&\sqrt{\left(\frac{1}{2}ab\right)^2 - \left(\frac{a^2 + b^2 - c^2}{4}\right)^2}\\=&\sqrt{\left(\frac{1}{2}ab + \frac{a^2 + b^2 - c^2}{4}\right)\left(\frac{1}{2}ab - \frac{a^2 + b^2 - c^2}{4}\right)}\\=&\sqrt{\frac{2ab + a^2 + b^2 - c^2}{4} \cdot \frac{2ab - a^2 - b^2 + c^2}{4}}\\=&\sqrt{\frac{(a + b)^2 - c^2}{4} \cdot \frac{c^2 - (a - b)^2}{4}}\\=&\sqrt{\frac{a + b + c}{2} \cdot \frac{a + b - c}{2} \cdot \frac{a + c - b}{2} \cdot \frac{b + c - a}{2}}\\=&\sqrt{p(p - a)(p - b)(p - c)}.\end{aligned} $
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦—秦九韶公式.
问题:如图,在$\triangle ABC$中,$AB = 13$,$BC = 12$,$AC = 7$,$\odot O内切于\triangle ABC$,切点分别是$D$,$E$,$F$.
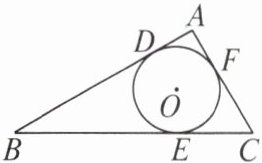
(1)求$\triangle ABC$的面积;
(2)求$\odot O$的半径.
材料:如果一个三角形的三边长分别为$a$,$b$,$c$,记$p = \frac{a + b + c}{2}$,那么三角形的面积为$S = \sqrt{p(p - a)(p - b)(p - c)}$. ①
古希腊几何学家海伦(Heron,约公元$50$年),在数学史上以解决几何测量问题而闻名. 他在《度量》一书中,给出了公式①和它的证明,这一公式称为海伦公式. 我国南宋数学家秦九韶(约$1202$ — 约$1261$),曾提出利用三角形的三边求面积的秦九韶公式$S = \sqrt{\frac{1}{4}\left[a^2b^2 - \left(\frac{a^2 + b^2 - c^2}{2}\right)^2\right]}$. ②
下面我们对公式②进行变形:
$\begin{aligned}&\sqrt{\frac{1}{4}\left[a^2b^2 - \left(\frac{a^2 + b^2 - c^2}{2}\right)^2\right]}\\=&\sqrt{\left(\frac{1}{2}ab\right)^2 - \left(\frac{a^2 + b^2 - c^2}{4}\right)^2}\\=&\sqrt{\left(\frac{1}{2}ab + \frac{a^2 + b^2 - c^2}{4}\right)\left(\frac{1}{2}ab - \frac{a^2 + b^2 - c^2}{4}\right)}\\=&\sqrt{\frac{2ab + a^2 + b^2 - c^2}{4} \cdot \frac{2ab - a^2 - b^2 + c^2}{4}}\\=&\sqrt{\frac{(a + b)^2 - c^2}{4} \cdot \frac{c^2 - (a - b)^2}{4}}\\=&\sqrt{\frac{a + b + c}{2} \cdot \frac{a + b - c}{2} \cdot \frac{a + c - b}{2} \cdot \frac{b + c - a}{2}}\\=&\sqrt{p(p - a)(p - b)(p - c)}.\end{aligned} $
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦—秦九韶公式.
问题:如图,在$\triangle ABC$中,$AB = 13$,$BC = 12$,$AC = 7$,$\odot O内切于\triangle ABC$,切点分别是$D$,$E$,$F$.

(1)求$\triangle ABC$的面积;
(2)求$\odot O$的半径.
答案:
(1)解 p=$\frac{AB+BC+AC}{2}$=$\frac{13+12+7}{2}$=16,
${S}_{\triangle ABC}=\sqrt{p(p - AB)(p - BC)(p - AC)}$
=$\sqrt{16×(16 - 13)×(16 - 12)×(16 - 7)}$
=$\sqrt{16×3×4×9}$
=24$\sqrt{3}$.
(2)连接OA,OB,OC,OD,OE,OF,

∵⊙O内切△ABC于点D,E,F,
∴OD⊥AB,OE⊥BC,OF⊥AC.
设⊙O的半径为r,
∵${S}_{\triangle ABC}={S}_{\triangle ABO}+{S}_{\triangle BCO}+{S}_{\triangle ACO}$,
∴${S}_{\triangle ABC}=\frac{AB·r}{2}+\frac{BC·r}{2}+\frac{AC·r}{2}$.
∴$\frac{13r}{2}+\frac{12r}{2}+\frac{7r}{2}$=24$\sqrt{3}$
∴r=$\frac{3\sqrt{3}}{2}$
(1)解 p=$\frac{AB+BC+AC}{2}$=$\frac{13+12+7}{2}$=16,
${S}_{\triangle ABC}=\sqrt{p(p - AB)(p - BC)(p - AC)}$
=$\sqrt{16×(16 - 13)×(16 - 12)×(16 - 7)}$
=$\sqrt{16×3×4×9}$
=24$\sqrt{3}$.
(2)连接OA,OB,OC,OD,OE,OF,

∵⊙O内切△ABC于点D,E,F,
∴OD⊥AB,OE⊥BC,OF⊥AC.
设⊙O的半径为r,
∵${S}_{\triangle ABC}={S}_{\triangle ABO}+{S}_{\triangle BCO}+{S}_{\triangle ACO}$,
∴${S}_{\triangle ABC}=\frac{AB·r}{2}+\frac{BC·r}{2}+\frac{AC·r}{2}$.
∴$\frac{13r}{2}+\frac{12r}{2}+\frac{7r}{2}$=24$\sqrt{3}$
∴r=$\frac{3\sqrt{3}}{2}$
查看更多完整答案,请扫码查看


