《2025年同步解析与测评学考练九年级数学上册人教版》

★7. 以半径为$1$的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)
A.$\frac{\sqrt{3}}{8}$
B.$\frac{\sqrt{3}}{4}$
C.$\frac{\sqrt{2}}{4}$
D.$\frac{\sqrt{2}}{8}$

答案： D

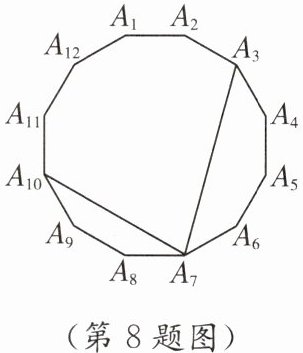
8. 如图,正十二边形$A_{1}A_{2}… A_{12}$,连接$A_{3}A_{7}$,$A_{7}A_{10}$,则$\angle A_{3}A_{7}A_{10} = $$75^{\circ}$。

答案： $75^{\circ}$

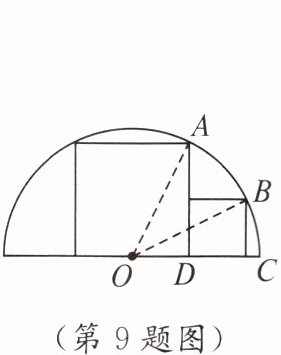
9. 如图,两个正方形彼此相邻且内接于半圆,若小正方形的面积为$16$ $cm^{2}$,则该半圆的半径为$4\sqrt{5}$cm。

答案： $4\sqrt{5}$

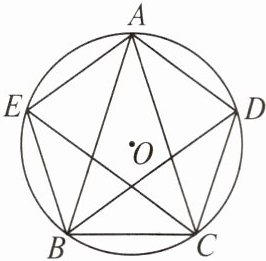
10. 如图,已知$\odot O的内接等腰三角形ABC$,$AB = AC$,弦$BD$,$CE分别平分\angle ABC$,$\angle ACB$,$BE = BC$,求证：五边形$AEBCD$是正五边形。

答案： 证明 在$\triangle ABC$中，$\because AB=AC,\therefore \angle ABC=\angle ACB.$ 又BD,CE分别平分$\angle ABC,\angle ACB,$ $\therefore \angle ABD=\angle DBC=\angle ACE=\angle ECB.$ $\therefore \overset{\frown}{AD}=\overset{\frown}{CD}=\overset{\frown}{AE}=\overset{\frown}{BE}.$ 又$BE=BC,\therefore \overset{\frown}{BE}=\overset{\frown}{BC},$ 即$\overset{\frown}{AD}=\overset{\frown}{DC}=\overset{\frown}{CB}=\overset{\frown}{BE}=\overset{\frown}{EA}.$ 故点A,E,B,C,D把$\odot O$五等分，即五边形AEBCD是正五边形.

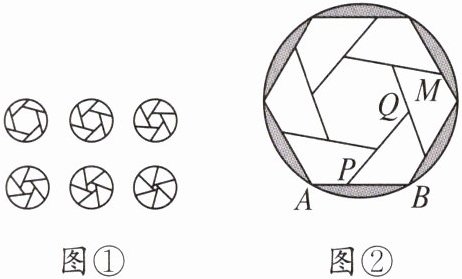
★11. 小明发现相机快门打开过程中,光圈大小变化如图①所示,于是他绘制了如图②所示的图形。图②中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若$PQ所在的直线经过点M$,$PB = 5$ cm,小正六边形的面积为$\frac{49\sqrt{3}}{2}$ $cm^{2}$,则该圆的半径为多少？

答案：
解 设两个正六边形的中心为O，如图，连接OP，OB，过点O作$OG\perp PM,OH\perp AB,MN$交圆内接正六边形于点N. 由题意得$\angle MNP=\angle NMP=\angle MPN=60^{\circ}.$ $\because$小正六边形的面积为$\frac{49\sqrt{3}}{2} cm^2,$ $\therefore$小正六边形的边长为$\frac{7\sqrt{3}}{3} cm,$ 即$PM=7\sqrt{3} cm.$ $\therefore S_{\triangle MPN}=\frac{1}{2}×7\sqrt{3}×7\sqrt{3}×\frac{\sqrt{3}}{2}=\frac{147\sqrt{3}}{4} cm^2.$ $\because OG\perp PM$，且O为正六边形的中心， $\therefore PG=\frac{1}{2}PM=\frac{7\sqrt{3}}{2} cm.$ 在$Rt\triangle OPG$中，根据勾股定理得 $OP=\sqrt{(\frac{7}{2})^2+(\frac{7\sqrt{3}}{2})^2}=7 cm.$ 设$OB=x cm$，$\because OH\perp AB$，且O为正六边形的中心，$\therefore BH=\frac{1}{2}x$，$OH=\frac{\sqrt{3}}{2}x$， $\therefore PH=(5-\frac{1}{2}x) cm.$ 在$Rt\triangle PHO$中， $OP^2=(\frac{\sqrt{3}}{2}x)^2+(5-\frac{1}{2}x)^2=49$， 解得$x=8$(负值舍去). $\therefore$该圆的半径为8 cm.