《2025年启东中学作业本八年级数学上册苏科版徐州专版》

7.如图,将一根长度为16cm自然伸直的弹性皮筋AB两端固定在水平的桌面上,然后把中点C竖直向上拉升6cm至点D,则该弹性皮筋被拉长了 (B)
A.2cm
B.4cm
C.6cm
D.8cm

答案： B

8.一艘船由A港沿北偏东$60^{\circ}$方向航行30km至B港,然后再沿北偏西$30^{\circ}$方向航行40km至C港,则A,C两港之间的距离为50km.

答案： 50

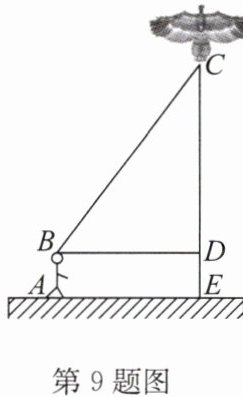
9.(吴中区期中)“儿童散学归来早,忙趁东风放纸鸢.”又到了放风筝的最佳时节.某校八年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:
①测得水平距离BD的长为15m;②根据手中剩余线的长度计算出风筝线BC的长为25m;③牵线放风筝的小明的身高为1.6m.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12m,那么他应该往回收线多少米?

答案：

(1)在Rt△CDB中,由勾股定理,得CD²=BC²−BD²=25²−15²=400,
∴CD=20.
∴CE=CD+DE=20+1.6=21.6(m).答:风筝的高度CE为21.6m
(2)如答图,由题意，得CM=12m,
∴DM=8m,
∴BM=√(DM²+BD²)= √(8²+15²)=17(m),
∴BC−BM=25−17=8(m).答:他应该往回收线8m.

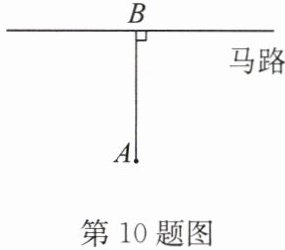
10.(建邺区期末)如图,点A处的居民楼与马路相距14m,当居民楼与马路上行驶的汽车距离小于50m时就会受到噪声污染,如果汽车以15m/s的速度行驶经过,那么会给这栋居民楼带来多长时间的噪声污染?

答案：
解:如答图，在马路上取点C,D,连接AC,AD,使AC=AD=50.根据题意可知，△ACD是等腰三角形，CD=2BC;在Rt△ABC中,AB=14,AC=50,由勾股定理知BC=√(AC²−AB²)= √(50²−14²)=48,所以CD=2BC=96.t=96÷15=6.4(s).答:会给这栋居民楼带来6.4s的噪声污染.

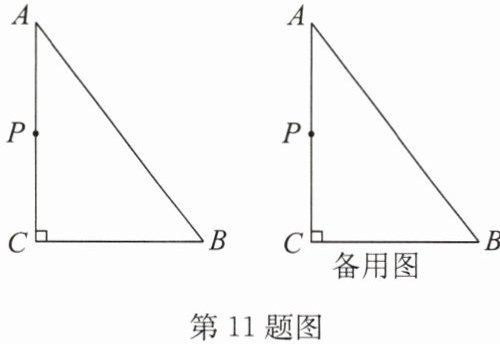
11.如图,在$\triangle ABC$中,$∠ACB= 90^{\circ},AB= 10,BC= 6$,若点P从点A出发,以每秒1个单位长度的速度沿$A→C→B→A$运动,设运动时间为t秒$(t＞0)$.
(1)若点P在AC上,且满足$PA= PB$,求此时t的值;
(2)若点P恰好在$∠BAC$的平分线上,求t的值.

答案：

(1)如答图①,连接PB.在Rt△ACB中,
∵AC²=AB²−BC²=10²−6²=64,
∴AC=8.由题意,得AP=t,则PB=t,PC=8−t.在Rt△PCB中,由勾股定理,得(8−t)²+6²=t²,解得t=25/4,即此时t的值为25/4.
(2)分两种情况:①当点P在BC上时,如答图②,过点P作PE⊥AB,则∠AEP=90°.由题意,得PC=t−8,PB=14−t
∵AP平分∠BAC,且∠ACB=90°,
∴PE=PC=t−8.
∵AP平分∠BAC,
∴∠CAP=∠BAP.在△ACP和△AEP中,{∠C=∠AEP,∠CAP=∠EAP,AP=AP,
∴△ACP≌△AEP(AAS),
∴AE=AC=8,
∴BE=2.在Rt△PEB中,由勾股定理,得PE²+EB²=PB²,即(t−8)²+2²=(14−t)²,解得t=32/3.②当点P又回到点A时，
∵AC+BC+AB=8+6+10=24,
∴t=24.综上所述，点P在∠BAC的平分线上时,t的值为32/3或24.