《2025年启东中学作业本八年级数学上册苏科版徐州专版》

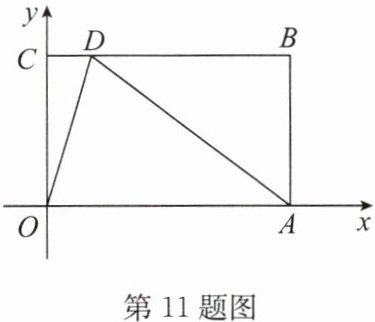
11.(14分)如图,在平面直角坐标系中,已知$A(10,0)$,$B(10,6)$,$BC\perp y$轴,垂足为$C$,点$D在线段BC$上,且$AD = AO$.
(1)求证：$DO平分\angle CDA$；
(2)求点$D$的坐标.

答案：
(1)证明:
∵BC⊥y轴,
∴BC//OA,
∴∠ODC=∠AOD.
∵AD=AO,
∴∠AOD=∠ADO,
∴∠ODC=∠ADO,
∴DO平分∠CDA.
(2)解:
∵A(10,0),B(10,6),
∴BC=OA=AD=10,AB=6.由勾股定理,得BD=√(AD²-AB²)=√(10²-6²)=8,
∴CD=BC-BD=10-8=2,
∴点D的坐标为(2,6).

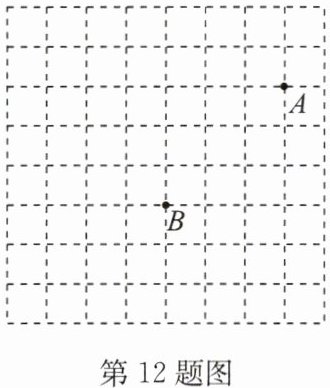
12.(18分)如图,每个小正方形的边长为1.已知在$\triangle ABC$中,点$A$,$B的坐标分别为(4,1)$,$(1,-2)$,$BC// x$轴,点$C在点B$右侧,且$BC = 2$.
(1)请根据已知条件,画出平面直角坐标系$xOy及\triangle ABC$,并写出点$C$的坐标；
(2)将$\triangle ABC$向左平移3个单位长度,再向上平移1个单位长度.按照这样的步骤平移后,如果$\triangle ABC上某一点P的对应点为P'(a,b)$,那么点$P$的坐标为______；(用含$a$,$b$的代数式表示)
(3)求$\triangle ABC$的面积.

答案：

(1)解:画出图形如答图所示,点C的坐标是(3,-2).
(2)(a+3,b-1)
(3)解:S△ABC=1/2 BC·(yA-yC)=1/2×2×[1-(-2)]=1/2×2×3=3.

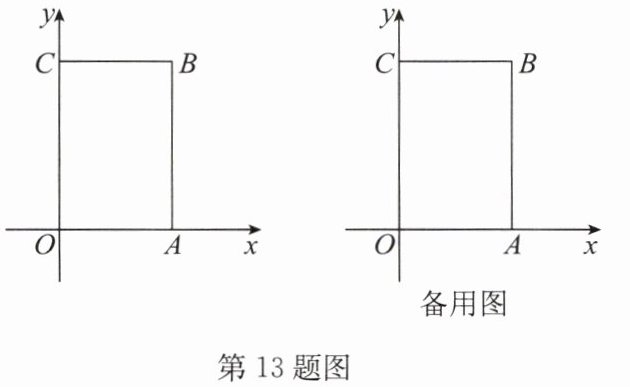
13.(18分)如图,在长方形$OABC$中,$O$为平面直角坐标系的原点,点$A的坐标为(a,0)$,点$C的坐标为(0,b)$,$a$,$b满足\sqrt{a - 8}+\vert b - 12\vert = 0$,点$B$在第一象限内,点$P$从原点出发,以每秒2个单位长度的速度沿$O\to A\to B\to C\to O$的线路移动.
(1)点$B$的坐标为______；当点$P$移动5秒时,点$P$的坐标为______；
(2)在移动过程中,当点$P$移动11秒时,求$\triangle OPB$的面积；
(3)在(2)的条件下,坐标轴上是否存在点$Q$,使$\triangle OPQ的面积与\triangle OPB$的面积相等？若存在,求点$Q$的坐标；若不存在,说明理由.

答案：

(1)(8,12) (8,2)
(2)解:如答图①. 当点P移动11秒时,11×2=22,
∵OA+AB=8+12=20＜22,OA+AB+BC=8+12+8=28＞22,
∴点P在边BC上,此时PB=22-20=2.
∴S△OPB=1/2 PB·OC=1/2×2×12=12.
(3)解:①如答图②,当点Q在x轴上时,
∵S△OPQ=1/2 OQ·BA=1/2 OQ×12=12,解得OQ=2,
∴Q(2,0)或Q(-2,0); ②如答图③,当点Q在y轴上时,
∵PB=2,BC=8,
∴CP=6.
∵S△OPQ=1/2 OQ·CP=1/2 OQ×6=12,解得OQ=4,
∴Q(0,4)或Q(0,-4).综上所述,存在点Q,使△OPQ的面积与△OPB的面积相等,其坐标为(2,0)或(-2,0)或(0,4)或(0,-4).