《2025年启东中学作业本八年级数学上册苏科版徐州专版》

11. (12分)某水果批发市场规定,批发苹果不少于100千克,批发价格为每千克2.5元. 小王携带现金300元到该市场采购苹果,并以批发价买进. 如果购买的苹果为$x$千克,小王付款后的剩余现金为$y$元.
(1)试写出$y与x$之间的函数表达式,并指出自变量的取值范围;
(2)画出相应的函数图象.

答案：
解:
(1)根据题意，得y与x之间的函数表达式为y=300−2.5x.
∵批发苹果不少于100千克时，批发价为每千克2.5元，
∴x≥100,且最多可以购买300÷2.5=120(千克).
故自变量x的取值范围是100≤x≤120.
综上所述，y与x之间的函数表达式为y=300-2.5x(100≤x≤120).
(2)由
(1)知,y=300−2.5x(100≤x≤120).
令x=100,则y=50;令x=120,则y=0.
画出的图象如答图.

12. (14分)已知一次函数$y= (2m+4)x+(3-n)$.
(1)当$m$＞−2,$n$＞3时,$y随x$的增大而增大,且函数图象与$y轴的交点在x$轴的下方;
(2)当$m$=−1,$n$≠6时,此函数图象平行于直线$y= 2x-3$;
(3)若$x$每增加1,$y$随之减小2,且此函数图象与两坐标轴围成的三角形的面积为4,求这个函数的表达式.
解:设该函数图象经过点T，点T的横坐标为t,则(2m+4)(t+1)+(3−n)−[(2m+4)t+(3−n)]=−2,
解得m=−3,故y=−2x+(3−n).
易得该函数图象与x轴的交点坐标为$(\frac{3−n}{2},0)$，与y轴的交点坐标为(0,3−n),则$\frac{1}{2}\cdot|\frac{3−n}{2}|\cdot|3−n|=4$,解得n=−1或n=7.
综上所述，这个函数的表达式为y=−2x+4或y=−2x−4.

答案：
(1)＞−2　＞3　
(2)=−1　≠6
(3)解:设该函数图象经过点T，点T的横坐标为t,则(2m+4)(t+1)+(3−n)−[(2m+4)t+(3−n)]=−2,
解得m=−3,故y=−2x+(3−n).
易得该函数图象与x轴的交点坐标为$(\frac{3−n}{2},0)$，与y轴的交点坐标为(0,3−n),则$\frac{1}{2}\cdot|\frac{3−n}{2}|\cdot|3−n|=4$,解得n=−1或n=7.
综上所述，这个函数的表达式为y=−2x+4或y=−2x−4.

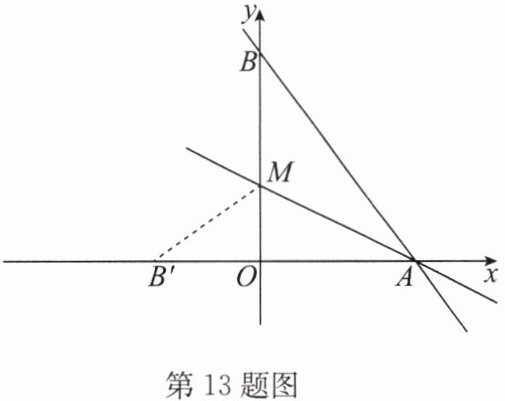
13. (14分)如图,直线$y= -\frac {4}{3}x+8与x$轴、$y轴分别交于点A和点B$,$M是OB$上的一点,若将$\triangle ABM沿AM$折叠,点$B恰好落在x轴上的点B'$处.
(1)求$A,B$两点的坐标;
(2)求直线$AM$的函数表达式;
(3)在$x轴上是否存在点P$,使得以点$P,M,B'$为顶点的三角形是等腰三角形? 若存在,请写出所有点$P$的坐标;若不存在,请说明理由.

答案：
解:
(1)当x=0时,y=8,
∴B(0,8).
当y=0时,$-\frac{4}{3}x+8=0$,解得x=6,
∴A(6,0).
(2)在Rt△AOB中,∠AOB=90°,OA=6,OB=8,
∴AB=10.由折叠得AB=AB'=10,
∴OB'=AB'-OA=10-6=4.
设OM=a,则BM=B'M=8-a,
在Rt△B'OM中,由勾股定理,得$a^{2}+4^{2}=(8-a)^{2}$,解得a=3.
∴M(0,3).
设直线AM的函数表达式为y=kx+b,
则$\begin{cases}6k + b = 0\\b = 3\end{cases}$，解得$\begin{cases}k = -\frac{1}{2}\\b = 3\end{cases}$
∴直线AM的函数表达式为$y=-\frac{1}{2}x+3$.
(3)在x轴上存在点P,使得以点P,M,B'为顶点的三角形是等腰三角形,如答图.

∵M(0,3),B'(-4,0),
∴B'M=5.
①当PB'=B'M时,P₁(-9,0),P₂(1,0).
②当B'M=PM时,P₃(4,0).
③当PB'=PM时,作B'M的垂直平分线,交x轴于点P₄,交B'M于点Q,则P₄M=P₄B',设P₄M=P₄B'=t,则OP₄=4-t.
在Rt△MOP₄中,由勾股定理,得$3^{2}+(4-t)^{2}=t^{2}$,解得$t=\frac{25}{8}$,
∴$OP_{4}=4-t=4-\frac{25}{8}=\frac{7}{8}$,
∴$P_{4}(-\frac{7}{8},0)$.
综上所述，点P的坐标为(-9,0)或(1,0)或(4,0)或$(-\frac{7}{8},0)$.