《2025年启东中学作业本八年级数学上册苏科版徐州专版》

11. (常熟期中)如图,在 $\triangle ABC$ 中, $AC = BC$, $\angle ACB = 120^{\circ}$,点 $D$ 在线段 $AB$ 上运动(点 $D$ 不与点 $A$, $B$ 重合),连接 $CD$,作 $\angle CDE = 30^{\circ}$, $DE$ 交 $BC$ 于点 $E$.若 $\triangle CDE$ 是等腰三角形,则 $\angle ADC$ 的度数是______60°或105°.

答案： 60°或１０５°

12. (江西模拟)如图,在等腰三角形 $ABC$ 中, $AB = AC$, $\angle B = 50^{\circ}$, $D$ 为 $BC$ 的中点,点 $E$ 在 $AB$ 上, $\angle AED = 70^{\circ}$.若 $P$ 是等腰三角形 $ABC$ 的腰上的一点,则当 $\triangle DEP$ 是以 $\angle EDP$ 为顶角的等腰三角形时, $\angle EDP$ 的度数是40°或100°或140°.

答案： 40°或100°或140°

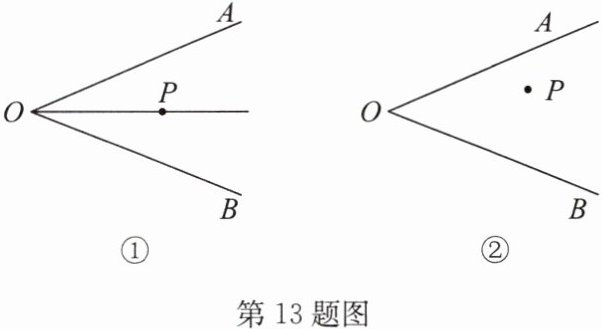
13. (1)如图①, $P$ 是 $\angle AOB$ 的平分线上一点,试过点 $P$ 画一条直线,交 $\angle AOB$ 的两边于点 $C$, $D$,使 $\triangle OCD$ 是等腰三角形,且 $CD$ 是底边;
(2)若点 $P$ 不在角平分线上,如图②,如何过点 $P$ 画直线与角的两边相交组成等腰三角形?
(3)问题(2)中能画出几个满足条件的等腰三角形?

答案：
解:
(1)如答图①,直线CD为OP的垂线且垂足为P,则△OCD是等腰三角形.理由如下:
∵OP为∠AOB的平分线，
∴∠AOP=∠BOP.
　又
∵OP=OP,∠CPO=∠DPO=90°,
∴△COP≌△DOP(ASA),
∴OC=OD,
∴△OCD是等腰三角形.
　
(2)如答图②,作∠AOB的平分线OC，过点P作PD⊥OC于点D,交OA,OB于点M,N,则△OMN为等腰三角形.理由如下:
∵OD为∠AOB的平分线,
∴∠AOD=∠BOD.
∵OD=OD,∠MDO=∠NDO=90°,
∴△MOD≌△NOD(ASA),
∴OM=ON,
∴△OMN是等腰三角形.
(3)①过点P作∠AOB的平分线的垂线，交OA,OB于点M,N,则△OMN是等腰三角形,如答图②.
　②过点P作OA的垂线,交OA,OB于点E,F,在EA上取点G,使EG=OE,连接FG,过点P作FG的平行线，交OA,OB于点M,N,则△OMN是等腰三角形,如答图③.
③过点P作OB的垂线,交OA,OB于点E,F,在FB上取点G,使FG=OF,连接EG,过点P作EG的平行线,交OA,OB于点M,N,则△OMN是等腰三角形,如答图④.
所以有三个满足条件的等腰三角形.

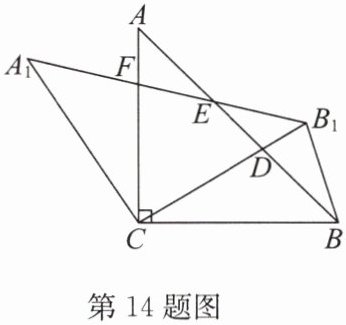
14. 如图,在 $\triangle ABC$ 中, $AC = BC$, $\angle ACB = 90^{\circ}$,将 $\triangle ABC$ 绕点 $C$ 逆时针旋转 $\alpha$ 角 $(0^{\circ} ＜ \alpha ＜ 90^{\circ})$,得到 $\triangle A_1B_1C$,连接 $BB_1$,设 $CB_1$ 交 $AB$ 于点 $D$, $A_1B_1$ 分别交 $AB$, $AC$ 于点 $E$, $F$.
(1)求证: $\triangle CBD \cong \triangle CA_1F$;
(2)试用含 $\alpha$ 的代数式表示 $\angle B_1BD$;
(3)当 $\alpha$ 等于多少度时, $\triangle BB_1D$ 是等腰三角形?

答案：
(1)证明:
∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转α角(0°＜α＜90°)得到△A₁B₁C,
∴∠A₁=∠A,A₁C=AC=BC,∠ACA₁=∠BCB₁=α,
∴∠A₁=∠CBD.
在△CBD和△CA₁F中,$\begin{cases} ∠CBD=∠CA₁F, \\ CB=CA₁, \\ ∠BCD=∠A₁CF, \end{cases}$
∴△CBD≌△CA₁F(ASA).
(2)解:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
由旋转的性质得BC=B₁C,
则∠CBB₁=∠CB₁B,
∴∠CB₁B=∠CBB₁=$\frac{180° -α}{2}$=90°-$\frac{α}{2}$,
∴∠B₁BD=∠CBB₁-∠CBA=90°-$\frac{α}{2}$-45°=45°-$\frac{α}{2}$.
(3)解:在△CBB₁中,
∵CB=CB₁,
∴∠CBB₁=∠CB₁B=$\frac{1}{2}$(180°−α).
又
∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B₁B=B₁D,则∠B₁DB=∠B₁BD.
∵∠B₁DB=45°+α,∠B₁BD=45°-$\frac{α}{2}$,
∴45°+α=45°-$\frac{α}{2}$,
∴α=0°(舍去);
②
∵∠BB₁C=∠B₁BC＞∠B₁BD,
∴BD≠B₁D;
③若BB₁=BD,则∠BDB₁=∠BB₁D,
即45°+α=$\frac{1}{2}$(180°−α),
∴α=30°.
综上可知，当△BB₁D为等腰三角形时,α=30°.