第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
6. [变式]在平面直角坐标系中,以原点为中心,把点A(2,-1)顺时针旋转90°得到点B的坐标为______.
答案:
$(-1,-2)$
7. 如图,点F在正方形ABCD的对角线AC上,连接BF,将BF绕点B逆时针旋转90°得到BE,连接AE,EF,求证:$AE^2+AF^2= 2BF^2.$


答案:
由上述推理可知$AE^{2}+AF^{2}=EF^{2}$且$EF^{2}=2BF^{2}$,所以$AE^{2}+AF^{2}=2BF^{2}$,得证。
8. □OABC在平面直角坐标系上的位置如图所示,其中点O,A,B,C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,-1).
(1)求□OABC的对称中心的坐标;
(2)求a+b的值.
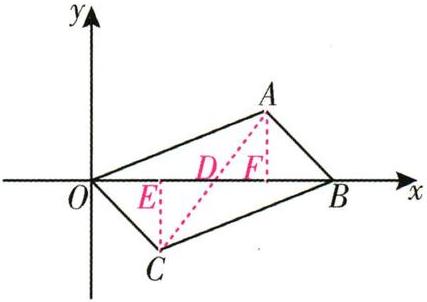
(1)求□OABC的对称中心的坐标;
(2)求a+b的值.

答案:
(1)$\square OABC$的对称中心的坐标为$\boldsymbol{(2,0)}$;
(2)$a + b$的值为$\boldsymbol{2}$。
(2)$a + b$的值为$\boldsymbol{2}$。
查看更多完整答案,请扫码查看


