《2025年活页过关练习西安出版社九年级数学上册人教版》

4. 小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量y(本)与销售单价x(元)之间满足一次函数关系,三对对应值如下表:

(1)y与x之间的函数解析式为______;
(2)通过与其他网店对比,小红将这款笔记本的单价定为x元($12\leqslant x\leqslant 15$,且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时,每周所获利润最大,最大利润是多少元?

答案：
(1)$y=-50x + 1100$；
(2)当销售单价定为$15$元时，每周所获利润最大，最大利润是$1750$元。

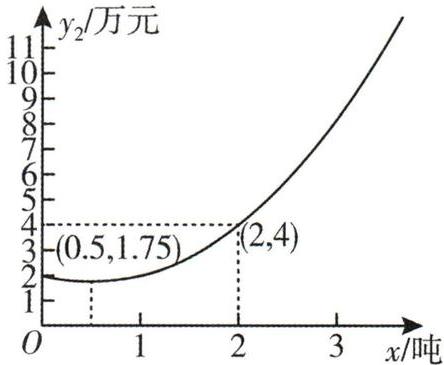
5. [2024新疆中考]某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额$y_{1}$(万元)与销售量x(吨)的函数解析式为$y_{1} = 5x$;成本$y_{2}$(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中$(0.5,1.75)$是其顶点.
(1)求出成本$y_{2}$关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?(注:利润= 销售额一成本)

答案：
(1) $y_{2}=x^{2}-x + 2$，$(0.4\leqslant x\leqslant3.5)$。
(2) 当成本最低时，销售产品所获利润是$0.75$万元。
(3) 当销售量是$3$吨时，可获得最大利润，最大利润是$7$万元。