《2025年活页过关练习西安出版社九年级数学上册人教版》

8. [变式]如图,A,B,C三点均在10×10的正方形网格的格点上.
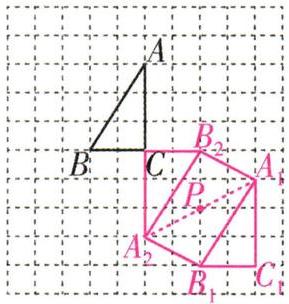
(1)画出将△ABC向右平移4格,再向下平移4格后的$△A_1B_1C_1；$
(2)画出将△ABC绕点C顺时针旋转180°后的$△A_2B_2C；$
(3)在(1)和(2)的条件下,四边形$A_1B_1A_2B_2$是否为中心对称图形？若是,请在图中标出它的对称中心P；若不是,请用所学知识简要说明理由.

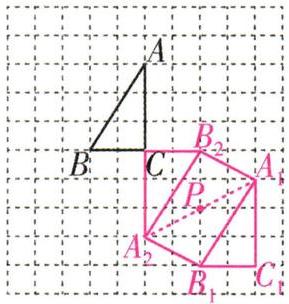
答案：
(1) 、
(2) 画图略。
(3) 四边形$A_1B_1A_2B_2$是中心对称图形，对称中心$P$为$A_1A_2$与$B_1B_2$的交点（图略）。

9. 将两个大小相等的圆部分重合,其中重叠的部分(如图中的阴影部分)我们称之为一个“花瓣”,

由一个“花瓣”及圆组成的图形称之为花瓣图形. 下面是一些由“花瓣”和圆组成的图形.
(1)在A,B,C,D,E这5个图形中,是轴对称图形的有______,是中心对称图形有______；
(2)设“花瓣”在圆中是均匀分布的,当花瓣数大于1时,若花瓣的个数是______,则花瓣图形既是轴对称图形又是中心对称图形；若花瓣的个数是______,则花瓣图形仅是轴对称图形；(填“奇数”或“偶数”)
(3)根据上面的结论,试判断下列花瓣图形是什么对称图形：
①九瓣图形是______；
②十二瓣图形是______.

答案： - （1）$A$、$B$、$C$、$D$、$E$；$A$、$C$、$E$。
（2）偶数；奇数。
（3）①轴对称图形；②既是轴对称图形又是中心对称图形。

10. 如图,在矩形ABCD中,AB= 1,BC= 2. 放入三个小正方形ANFM,EFGH,HPCQ后形成一个中心对称图形,求此三个小正方形的面积之和.

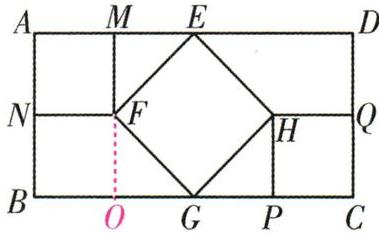
答案： 此三个小正方形的面积之和为$\boldsymbol{1}$。