《2025年活页过关练习西安出版社九年级数学上册人教版》

1. [典型习题] 如果两个图形关于某一点成中心对称,下列说法：①这两个图形一定是全等图形；②对称点的连线一定经过对称中心；③将一个图形绕对称中心旋转某个角度必定与另一个图形重合；④一定存在某直线,沿该直线折叠后的两个图形互相重合.其中正确的是______. (填序号)

答案： ①②

2. [变式][2024集美模拟] 下列各组图形中,$\triangle A^{\prime} B^{\prime} C^{\prime}与\triangle A B C$成中心对称的是()
A.
B.
C.
D.

答案： C

3. [变式] 如图,$\square A B C D的对角线A C$,$B D交于点O$,则图中成中心对称的三角形共有______对.

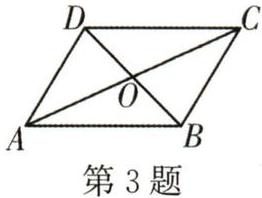
答案： $4$

4. [典型习题] 如图,若四边形$A B C D与四边形F G C E$成中心对称,则它们的对称中心是点______,点$A$的对称点是点______,点$E$的对称点是点______,$B D //$______且$B D= $______,$\triangle A B D \cong$______.若连接$A F$,则$A F$经过点______且被该点______.

答案： $C$；$F$；$D$；$EG$；$EG$；$\triangle FGE$；$C$；平分

5. [变式][2024武夷山月考] 如图,$\triangle A G B与\triangle C G D关于点G$中心对称,若点$E$,$F分别在G A$,$G C$上,且$A F= C E$. 求证：$B F= D E$.

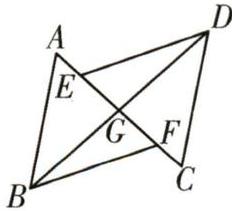
答案： $\because\triangle AGB$与$\triangle CGD$关于点$G$中心对称，
$\therefore AG = CG$，$BG = DG$。
$\because AF = CE$，
$\therefore AG - AF = CG - CE$，即$GF = GE$。
在$\triangle BGF$和$\triangle DGE$中，
$\begin{cases}BG = DG\\\angle BGF=\angle DGE\\GF = GE\end{cases}$
$\therefore\triangle BGF\cong\triangle DGE(SAS)$。
$\therefore BF = DE$ 。

6. [典型习题] 如图,$\triangle A B C与\triangle A_{1} B_{1} C_{1}关于点O$对称,其中$A$,$A_{1}$为对称点,画出点$O和\triangle A_{1} B_{1} C_{1}$.

答案： 按照上述步骤画出点$O$和$\triangle A_{1}B_{1}C_{1}$（具体图形根据上述作图方法绘制）。

7. [变式][2024仓山期中] 如图,$\triangle A B C和\triangle D E F关于点O$成中心对称.
(1) 找出它们的对称中心$O$；
(2) 若$A B= 7$,$A C= 5$,$B C= 6$,求$\triangle D E F$的周长.

答案：
(1) 连接 $AD$、$CF$，交点即为对称中心 $O$。
(2) $\triangle DEF$的周长为$\boldsymbol{18}$。