2025年通城学典非常课课通九年级数学下册苏科版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学下册苏科版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第173页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
典例3(东海一模)如图①,一艘渔船位于观测站A的北偏东53.2°方向的点B处,它沿正南方向航行,航行15 n mile后,观察站A测得该渔船位于南偏东63.4°方向的点D处.
(1)求证:BA = BD;
(2)若渔船从点D处继续按着原方向航行(12√3 - 6)n mile后到达点C时突然发生事故,渔船马上向观测站A处的救援队求救,救援队从点A处出发沿着哪个方向航行到达事故地点C的航程最短(参考数据:sin53.2°≈0.80,cos53.2°≈0.60)?
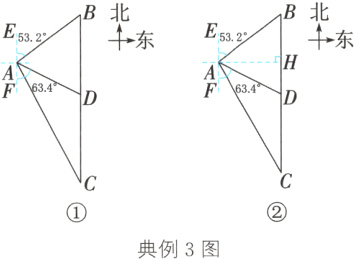
解析:(1)因为BD与BA都在△ABD中,所以可先分别求出它们所对的∠BAD和∠ADB的度数,然后证∠BAD = ∠ADB.(2)根据两点之间线段最短,可知线段AC的长就是到达事故地点最短的航程,故求出AC与正南方向的夹角∠FAC即可. 由于易得AF//BC,故考虑把∠FAC转化成∠C. 过点A作AH⊥BC于点H,分别解Rt△ABH、Rt△ACH,可求∠C的度数.
解:(1)根据题意,易得∠FAD = ∠ADB = 63.4°,∠EAB = ∠B = 53.2°. ∴∠BAD = 180° - ∠EAB - ∠FAD = 180° - 53.2° - 63.4° = 63.4°. ∴∠BAD = ∠ADB. ∴BA = BD.
(2)如图②,过点A作AH⊥BC于点H. 根据题意,得AB = BD = 15 n mile,CD = (12√3 - 6)n mile. 在Rt△ABH中,
∵∠AHB = 90°,∴sinB = AH/AB,cosB = BH/AB.
∴AH≈12 n mile,BH≈9 n mile. ∴HD = BD - BH = 15 - 9 = 6(n mile). ∴CH = HD + CD = 6 + (12√3 - 6) = 12√3(n mile). 在Rt△ACH中,∵∠AHC = 90°,∴tanC = AH/CH = 12/(12√3) = √3/3. ∵由题意,得∠C为锐角,
∴∠C = 30°. ∵易得AF//BC,∴∠FAC = ∠C = 30°. ∴救援队从点A处出发沿着南偏东30°方向航行到达事故地点C的航程最短.
(1)求证:BA = BD;
(2)若渔船从点D处继续按着原方向航行(12√3 - 6)n mile后到达点C时突然发生事故,渔船马上向观测站A处的救援队求救,救援队从点A处出发沿着哪个方向航行到达事故地点C的航程最短(参考数据:sin53.2°≈0.80,cos53.2°≈0.60)?

解析:(1)因为BD与BA都在△ABD中,所以可先分别求出它们所对的∠BAD和∠ADB的度数,然后证∠BAD = ∠ADB.(2)根据两点之间线段最短,可知线段AC的长就是到达事故地点最短的航程,故求出AC与正南方向的夹角∠FAC即可. 由于易得AF//BC,故考虑把∠FAC转化成∠C. 过点A作AH⊥BC于点H,分别解Rt△ABH、Rt△ACH,可求∠C的度数.
解:(1)根据题意,易得∠FAD = ∠ADB = 63.4°,∠EAB = ∠B = 53.2°. ∴∠BAD = 180° - ∠EAB - ∠FAD = 180° - 53.2° - 63.4° = 63.4°. ∴∠BAD = ∠ADB. ∴BA = BD.
(2)如图②,过点A作AH⊥BC于点H. 根据题意,得AB = BD = 15 n mile,CD = (12√3 - 6)n mile. 在Rt△ABH中,
∵∠AHB = 90°,∴sinB = AH/AB,cosB = BH/AB.
∴AH≈12 n mile,BH≈9 n mile. ∴HD = BD - BH = 15 - 9 = 6(n mile). ∴CH = HD + CD = 6 + (12√3 - 6) = 12√3(n mile). 在Rt△ACH中,∵∠AHC = 90°,∴tanC = AH/CH = 12/(12√3) = √3/3. ∵由题意,得∠C为锐角,
∴∠C = 30°. ∵易得AF//BC,∴∠FAC = ∠C = 30°. ∴救援队从点A处出发沿着南偏东30°方向航行到达事故地点C的航程最短.
答案:
典例4 某市政府为了方便市民绿色出行,推出了共享单车服务. 如图①所示为某品牌共享单车放在水平地面上的实物图,如图②所示为其示意图,其中AB、CD都与地面l平行,车轮的半径为32 cm,∠BCD = 64°,BC = 60 cm,坐垫E与点B的距离BE为15 cm(精确到0.1 cm,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05).
(1)求坐垫E到地面的距离.
(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适. 小明的腿长约为80 cm,现将坐垫E调整至坐骑舒适高度位置E′,求EE′的长.


解析:(1)过点E作EM⊥CD于点M,延长EM交l于点N,则点E到地面的距离为EN的长,可转化成EM与MN的和来求.(2)由于EE′ = CE - CE′,CE为已知线段,故要求EE′的长只需求CE′的长,考虑过点E′作E′H⊥CD于点H,在Rt△CE′H中求CE′的长.
解:(1)如图③,过点E作EM⊥CD于点M,延长EM交l于点N,设l与⊙D相切于点G,连接DG. 根据题意,得∠BCM = 64°,DG = 32 cm,CE = BC + BE = 60 + 15 = 75(cm). ∵CD//l,EM⊥CD,∴MN⊥l.
∴MN = DG = 32 cm. 在Rt△CEM中,
∵∠CME = 90°,∴EM = CE·sin∠BCM = 75×sin64°≈67.5(cm). ∴EN = EM + MN = 99.5 cm. ∴坐垫E到地面的距离约为99.5 cm.
(2)如图③,过点E′作E′H⊥CD于点H. 根据题意,得E′H≈80×0.8 = 64(cm). 在Rt△CE′H中,∵∠CHE′ = 90°,∴CE′ = E′H/sin∠BCM ≈ 71.11 cm. ∴EE′ = CE - CE′≈3.9 cm. ∴EE′的长约为3.9 cm.
(1)求坐垫E到地面的距离.
(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适. 小明的腿长约为80 cm,现将坐垫E调整至坐骑舒适高度位置E′,求EE′的长.


解析:(1)过点E作EM⊥CD于点M,延长EM交l于点N,则点E到地面的距离为EN的长,可转化成EM与MN的和来求.(2)由于EE′ = CE - CE′,CE为已知线段,故要求EE′的长只需求CE′的长,考虑过点E′作E′H⊥CD于点H,在Rt△CE′H中求CE′的长.
解:(1)如图③,过点E作EM⊥CD于点M,延长EM交l于点N,设l与⊙D相切于点G,连接DG. 根据题意,得∠BCM = 64°,DG = 32 cm,CE = BC + BE = 60 + 15 = 75(cm). ∵CD//l,EM⊥CD,∴MN⊥l.
∴MN = DG = 32 cm. 在Rt△CEM中,
∵∠CME = 90°,∴EM = CE·sin∠BCM = 75×sin64°≈67.5(cm). ∴EN = EM + MN = 99.5 cm. ∴坐垫E到地面的距离约为99.5 cm.
(2)如图③,过点E′作E′H⊥CD于点H. 根据题意,得E′H≈80×0.8 = 64(cm). 在Rt△CE′H中,∵∠CHE′ = 90°,∴CE′ = E′H/sin∠BCM ≈ 71.11 cm. ∴EE′ = CE - CE′≈3.9 cm. ∴EE′的长约为3.9 cm.
答案:
查看更多完整答案,请扫码查看


