《2025年综合应用创新题典中点九年级数学下册鲁教版》

7. 母题教材P79习题T2如图，在边长为12 cm的等边三角形ABC中，点P从点A开始沿AB边向点B以1 cm/s的速度移动，点Q从点B开始沿BC边向点C以2 cm/s的速度移动. 若P，Q两点同时出发，其中任意一点到达目的地后，两点同时停止运动，则经过________s后，△BPQ的面积等于10√3 cm².
　　　　　　　　　　　　　　

答案： 2【点拨】设经过$x\ s$后$\triangle BPQ$的面积等于$10\sqrt{3}\ cm^{2}$，则$AP = x\ cm$，$BQ = 2x\ cm$，过点$Q$作$QD\perp AB$，垂足为$D$，则$\angle BDQ = 90^{\circ}$，$\because$等边三角形$ABC$中，$AB = 12\ cm$，$\angle B = 60^{\circ}$，$\therefore PB = (12 - x)cm$，$\angle BQD = 90^{\circ}-\angle B = 30^{\circ}$，$\therefore BD = \frac{1}{2}BQ = x\ cm$，$\therefore DQ = \sqrt{BQ^{2}-BD^{2}}=\sqrt{3}x\ cm$，$\therefore \frac{1}{2}×(12 - x)×\sqrt{3}x = 10\sqrt{3}$，解得$x_{1}=10$(不合题意,舍去)，$x_{2}=2$，$\therefore x = 2$，则经过$2\ s$后$\triangle BPQ$的面积等于$10\sqrt{3}\ cm^{2}$。

8. [2024·德州模拟]如图，A，B，C，D为矩形的四个顶点，AB = 16 cm，AD = 6 cm，动点P，Q分别从点A，C同时出发，点P以3 cm/s的速度向点B移动，一直到达B点停止，点Q以2 cm/s的速度向D点移动，当点P到达B点时点Q随之停止移动，设移动时间为t s.
(1)AP = ______，BP = ______，CQ = ______，DQ = ______（用含t的代数式表示）；
(2)当t为多少时，四边形PBCQ的面积为33 cm²；
(3)当t为多少时，点P和点Q的距离为10 cm.
　　　　　　　　　　　　　　　　

答案： 【解】
(1)$3t\ cm$；$(16 - 3t)\ cm$；$2t\ cm$；$(16 - 2t)\ cm$。
(2)依题意，得$\frac{1}{2}[(16 - 3t)+2t]×6 = 33$，整理得$16 - t = 11$，解得$t = 5$。答：当$t$为$5$时，四边形$PBCQ$的面积为$33\ cm^{2}$。
(3)过点$Q$作$QE\perp AB$于点$E$，则$PE = |(16 - 3t)-2t| = |16 - 5t|\ cm$，依题意得$(16 - 5t)^{2}+6^{2}=10^{2}$，即$(16 - 5t)^{2}=8^{2}$，解得$t_{1}=\frac{8}{5}$，$t_{2}=\frac{24}{5}$。答：当$t$为$\frac{8}{5}$或$\frac{24}{5}$时，点$P$和点$Q$的距离为$10\ cm$。

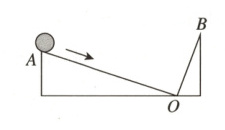
9. 新趋势 跨学科如图，钢球（不计大小）在一个光滑的“V”型轨道上滚动（表面光滑，摩擦阻力不计），其中左侧轨道AO长为32 cm，右侧轨道BO长为20 cm. 钢球先由A点静止开始沿左侧轨道滚下，速度每秒增加4 cm/s，到达底端O后又沿着右侧轨道向上滚动，速度每秒减少6 cm/s.（提示：在同一侧轨道上，钢球滚动的距离 = 平均速度v̅×时间t，v̅ = (v₀ + vₜ)/2，其中v₀表示开始的速度，vₜ表示t秒时的速度. ）
(1)当钢球滚动4 s时，它的速度为______cm/s，经过的路程是______cm.
(2)经过多少秒后，钢球到最低点O的距离为16 cm？

答案： 【解】
(1)$16$；$32$【点拨】当钢球滚动$4\ s$时，它的速度为$4×4 = 16(cm/s)$，$\overline{v}=\frac{v_{0}+v_{t}}{2}=\frac{0 + 16}{2}=8(cm/s)$，经过的路程是$8×4 = 32(cm)$。
(2)设经过$b\ s$后，钢球在右侧轨道$BO$的滚动速度等于$0$，由
(1)可知，当钢球从点$A$滚动到点$O$时，滚动时间为$4\ s$，速度为$16\ cm/s$，则$16 - 6(b - 4)=0$，解得$b=\frac{20}{3}$。设经过$x\ s$后，钢球到最低点$O$的距离为$16\ cm$，由题意，分以下两种情况：①当钢球在左侧轨道$AO$上时，则$\frac{0 + 4x}{2}×x = 32 - 16$，解得$x = 2\sqrt{2}$或$x = -2\sqrt{2}＜0$(不符合题意，舍去)；②当钢球在右侧轨道$BO$上时，则$\frac{16 + 16 - 6(x - 4)}{2}×(x - 4)=16$，解得$x=\frac{16}{3}$或$x = 8＞\frac{20}{3}$(不符合题意，舍去)。综上，经过$2\sqrt{2}\ s$或$\frac{16}{3}\ s$后，钢球到最低点$O$的距离为$16\ cm$。