搜索
第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [2024·常州]起重机将1000N的重物先竖直向上匀速提升3m,再悬停6s,起重机对重物做功情况是(
A.提升过程做了功,悬停过程做了功
B.提升过程不做功,悬停过程不做功
C.提升过程不做功,悬停过程做了功
D.提升过程做了功,悬停过程不做功
D
)A.提升过程做了功,悬停过程做了功
B.提升过程不做功,悬停过程不做功
C.提升过程不做功,悬停过程做了功
D.提升过程做了功,悬停过程不做功
答案：
D [点拨]做功的两个必要条件:
(1)有力作用在物体上;
(2)物体在力的方向上移动一段距离。故起重机匀速提升重物过程中对重物做功,悬停过程中对重物不做功，故D符合题意。
(1)有力作用在物体上;
(2)物体在力的方向上移动一段距离。故起重机匀速提升重物过程中对重物做功,悬停过程中对重物不做功，故D符合题意。
2. [2025·六安阶段练习]如图是环保卫士小安在进行垃圾分类,下列环节中,小安对瓶子做功的行为是(
A.从地上拾起瓶子
B.手握瓶子沿水平方向走到垃圾桶旁
C.一只手握瓶子不动,另一只手打开垃圾桶桶盖
D.瓶子离开手,掉入垃圾桶中
A
)A.从地上拾起瓶子
B.手握瓶子沿水平方向走到垃圾桶旁
C.一只手握瓶子不动,另一只手打开垃圾桶桶盖
D.瓶子离开手,掉入垃圾桶中
答案：
A [点拨]从地上拾起瓶子,小安对瓶子有竖直向上的力，瓶子在力的方向上移动了距离，小安对瓶子做了功，故A符合题意;BC中，小安对瓶子有竖直向上的力，瓶子在力的方向上没有移动距离，小安对瓶子不做功;D中，瓶子离开手后，小安对瓶子不再施加力的作用，对瓶子不做功,故D不符合题意。故选A。
3. 如图所示,物体在相同力F的作用下,分别在光滑水平面、粗糙水平面和粗糙斜面上沿着力的方向移动了相同的距离s,力F做的功分别为$W_1、$$W_2、$$W_3,$比较甲、乙、丙三次所做的功的大小(
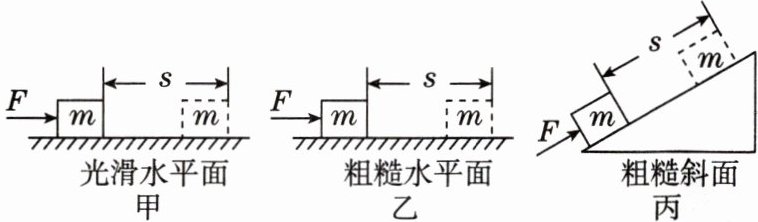
$A. W_1 = W_2 = W_3$
$B. W_1 ＞ W_2 ＞ W_3$
$C. W_1 ＜ W_2 ＜ W_3$
$D. 无法判定$
A
)$A. W_1 = W_2 = W_3$
$B. W_1 ＞ W_2 ＞ W_3$
$C. W_1 ＜ W_2 ＜ W_3$
$D. 无法判定$
答案：
A [点拨]由题知,力大小相同，沿力的方向移动的距离相同,根据W=Fs可得,力F做的功$W_{1}=W_{2}=W_{3}$。
4. 功的计算公式是
(1)若人用20N的水平拉力,拉着重为50N的爬犁在水平冰面上匀速滑行3m,爬犁重力做功为
(2)若水平拉力突然增大为30N,爬犁将做
(3)在此后,牵引爬犁的绳子突然断了,爬犁靠惯性向前运动了10m,此阶段拉力做功为
W=Fs
。(1)若人用20N的水平拉力,拉着重为50N的爬犁在水平冰面上匀速滑行3m,爬犁重力做功为
0
J,人的水平拉力做功为60
J。(2)若水平拉力突然增大为30N,爬犁将做
加速运动
(填“匀速运动”“加速运动”或“减速运动”),假设爬犁在此阶段又运动了5m,此时,水平拉力变化前后总共做功为210
J。(3)在此后,牵引爬犁的绳子突然断了,爬犁靠惯性向前运动了10m,此阶段拉力做功为
0
J。
答案：
W=Fs
(1)0;60
(2)加速运动;210
(3)0 [点拨]
(1)重力的方向和运动方向垂直，重力做功为0J;水平拉力做功$W_{1}=F_{1}s_{1}=20N× 3m=60J$。
(2)$W_{2}=F_{2}s_{2}=30N× 5m=150J$，$W=W_{1}+W_{2}=60J+150J=210J$。
(3)此阶段爬犁不受拉力，拉力做功为0J。
(1)0;60
(2)加速运动;210
(3)0 [点拨]
(1)重力的方向和运动方向垂直，重力做功为0J;水平拉力做功$W_{1}=F_{1}s_{1}=20N× 3m=60J$。
(2)$W_{2}=F_{2}s_{2}=30N× 5m=150J$，$W=W_{1}+W_{2}=60J+150J=210J$。
(3)此阶段爬犁不受拉力，拉力做功为0J。
5. 克服重力做功：若一个物体受到竖直向下的重力G,且逆着重力的方向运动的距离为h,我们就说这种情况是“克服重力做了功”,或者叫做“克服重力做功”,且做功的大小利用公式W = Gh计算。
克服摩擦力做功：若一个物体受到某个方向的摩擦力f,且逆着摩擦力的方向运动的距离为s,我们就说这种情况是“克服摩擦力做了功”,或者叫做“克服摩擦力做功”,且做功的大小利用公式W = fs计算。
拓展训练我国独立设计制造的机械手臂,已经投入工业生产。如图所示,机械手臂(未画出)用力将一重为20N的木块从长为5m、高为2m的斜面底端匀速拉到斜面顶端。若木块与斜面间的摩擦力为10N,则这个机械手臂克服木块的重力做的功为
]
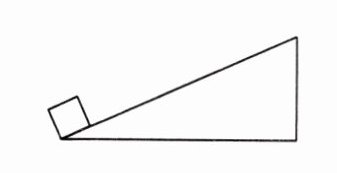
克服摩擦力做功：若一个物体受到某个方向的摩擦力f,且逆着摩擦力的方向运动的距离为s,我们就说这种情况是“克服摩擦力做了功”,或者叫做“克服摩擦力做功”,且做功的大小利用公式W = fs计算。
拓展训练我国独立设计制造的机械手臂,已经投入工业生产。如图所示,机械手臂(未画出)用力将一重为20N的木块从长为5m、高为2m的斜面底端匀速拉到斜面顶端。若木块与斜面间的摩擦力为10N,则这个机械手臂克服木块的重力做的功为
40
J,克服木块与斜面间摩擦力做的功为50
J,机械手臂克服木块的重力和木块受到的摩擦力一共做了90
J的功。]
答案：
40;50;90 [点拨]克服木块的重力做的功$W_{G}=Gh=20N× 2m=40J$，克服木块与斜面间摩擦力做的功$W_{f}=fs=10N× 5m=50J$；机械手臂克服木块的重力和木块受到的摩擦力一共做功$W=W_{G}+W_{f}=40J+50J=90J$。
6. 跨学科日常生活会干不如巧干,搬东西要讲技巧。一块厚度、密度均匀的长方体水泥板放在水平地面上,用一竖直向上的力,将其抬起时所用力的两种情况如图所示,抬至竖直位置所做的功分别为Wₐ、Wᵦ,则( )
A.Fₐ ＞ Fᵦ,Wₐ ＞ Wᵦ
B.Fₐ ＜ Fᵦ,Wₐ = Wᵦ
C.Fₐ = Fᵦ,Wₐ ＜ Wᵦ
D.Fₐ ＞ Fᵦ,Wₐ ＜ Wᵦ
A.Fₐ ＞ Fᵦ,Wₐ ＞ Wᵦ
B.Fₐ ＜ Fᵦ,Wₐ = Wᵦ
C.Fₐ = Fᵦ,Wₐ ＜ Wᵦ
D.Fₐ ＞ Fᵦ,Wₐ ＜ Wᵦ
答案：
C [点拨]两次抬起水泥板时的情况如图所示:
在上述两种情况下,动力克服的都是水泥板的重力，形状规则、质量均匀的物体，其重心都在其几何中心上，所以阻力臂都等于动力臂的$\frac{1}{2}$，根据杠杆的平衡条件可得，抬水泥板所用的力$F=\frac{GL_{阻}}{L_{动}}=\frac{1}{2}G$，即两种情况所需力的大小$F_{甲}=F_{乙}$；若甲、乙两种情况均将水泥板抬至竖直位置，由题图可知重心提升高度$h_{甲}＜h_{乙}$，则$W_{甲}=Gh_{甲}＜Gh_{乙}=W_{乙}$，故C符合题意。
C [点拨]两次抬起水泥板时的情况如图所示:
在上述两种情况下,动力克服的都是水泥板的重力，形状规则、质量均匀的物体，其重心都在其几何中心上，所以阻力臂都等于动力臂的$\frac{1}{2}$，根据杠杆的平衡条件可得，抬水泥板所用的力$F=\frac{GL_{阻}}{L_{动}}=\frac{1}{2}G$，即两种情况所需力的大小$F_{甲}=F_{乙}$；若甲、乙两种情况均将水泥板抬至竖直位置，由题图可知重心提升高度$h_{甲}＜h_{乙}$，则$W_{甲}=Gh_{甲}＜Gh_{乙}=W_{乙}$，故C符合题意。 查看更多完整答案，请扫码查看
